Question
When is bombarded with one neutron, the following
fission reaction occurs:
- Find the values for x and y.
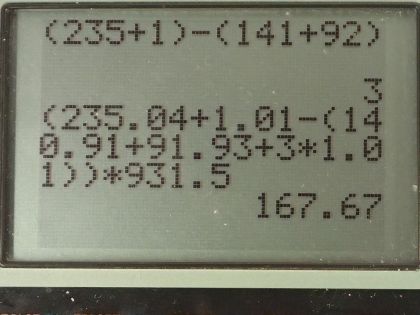
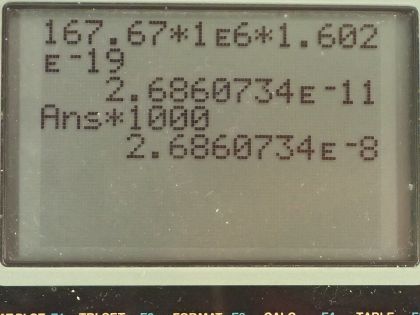
- Assuming that the mass of is 235.04 u, the mass of is 140.91 u, the mass of is 91.93 u, and the mass of is 1.01 u, a student calculates the energy released in the fission reaction as , but forgets to write the unit. Find the correct unit and convert the answer to MeV.
Final Answer
- ,
- . The missing units are
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 10 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An uranium-235 nuclide is bombarded with a single neutron turning it into barium-141 and krypton-92 and some neutrons and the question is how many neutrons— what is x in other words— and what is the atomic number of krypton is this question essentially because y is the number of protons, which is the atomic number. So let's look up atomic number of krypton first and it is 36 so y is 36 and x is the number of nucleons that are unaccounted for among these two daughter nuclides we need to have a total of 235 plus 1 nucleons because there are 235 nucleons in this uranium nuclide plus the 1 nucleon here and then take away from that the 141 accounted for in the barium plus the 92 accounted for in the krypton and that leaves 3 left over, there are 3 neutrons produced. Part (b) asks what is the energy created in megaelectron volts and also what are the units of this number which is also the energy but we don't know what the units are. So first we will calculate our answer in megaelectron volts. The energy is the mass defect or the difference in mass between the reactants and the products times c squared and so that's the mass of uranium-235 plus the mass of a neutron on the left side of the equation here and then from that take the total mass on the right side, which is the mass of barium-141 and the mass of krypton-92 and the mass of three neutrons. So we are given the masses of all these things which is convenient and we plug in some numbers now. So that's 235.04 atomic mass units for uranium-235 plus 1.01 atomic mass units for a neutron minus 140.91 plus 91.93 plus 3 times 1.01 and we convert all that into megaelectron volts per c squared by multiplying by 931.5 and then times c squared and we end up with 168 megaelectron volts and now we will do some guessing and checking to convert this energy into different units to see if we can create this number here so let's see if it's joules. We'll multiply by 1 times 10 to the 6 electron volts for every megaelectron volt and then by 1.602 times 10 to the minus 19 joules per electron volt and that gives 2.686 times 10 to the minus 11 joules and that's almost the right number we can ignore differences in this digit here since that's probably a rounding error but we need 10 to the minus 8 instead of 10 to the minus 11. So if we multiply by 1000 millijoules for every joule, we now get 10 to the minus 8, the units are millijoules.