Question
Suppose two deuterium nuclei are fused to produce helium.
- Write the equation for the fusion reaction.
- Calculate the difference between the masses of reactants and products.
- Using the result calculated in (b), find the energy produced in the fusion reaction.
Final Answer
- Please see the solution video
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 6 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
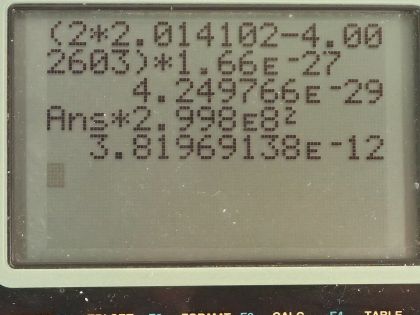
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Suppose two deuterium nuclei are fused to produce helium, we have to, in part (a), write the equation for the fusion reaction so deuterium is a proton combined with a neutron so there are two nucleons so it's hydrogen-2 in other words plus another hydrogen-2 creates a helium-4 because there has to be four nucleons in this helium and being helium means its atomic number is 2 so definitely has 2 protons and with 4 nucleons and 2 protons, there must be 2 neutrons in it. There's also a γ ray produced... this part isn't obvious from conservation laws, it's just something there as a way to release this energy... there's a lot of energy being released and it has to be released somehow and it's released in the form of kinetic energy of the helium nuclide but also in the form of gamma radiation. Part (b) asks for the difference in masses between the reactants and products. So there are two deuterium nuclides and this is the atomic mass which includes the mass of the electron surrounding the deuterium nuclide but that's fine because there are also two electron masses included in this helium atomic mass and so those electron masses will subtract away. So we have two times the atomic mass of deuterium minus the atomic mass of helium converted into kilograms by multiplying by 1.66 times 10 to the minus 27 kilograms per atomic mass unit and we have 4.25 times 10 to the minus 29 kilograms. Part (c) asks us to find the energy produced in the reaction. So the energy is the mass lost or the mass defect multiplied by c squared. So that's our answer for part (b) multiplied by the speed of light squared and that's 3.82 times 10 to the minus 12 joules.