Question
Some of the most powerful lasers are based on the energy levels of neodymium in solids, such as glass, as shown in Figure 30.65. (a) What average wavelength light can pump the neodymium into the levels above its metastable state? (b) Verify that the 1.17 eV transition produces 1.06 μm1.06\textrm{ }\mu\textrm{m} radiation.
<b>Figure 30.65</b> Neodymium atoms in glass have these energy levels, one of which is metastable. The group of levels above the metastable state is convenient for achieving a population inversion, since photons of many different energies can be absorbed by atoms in the ground state.
Figure 30.65 Neodymium atoms in glass have these energy levels, one of which is metastable. The group of levels above the metastable state is convenient for achieving a population inversion, since photons of many different energies can be absorbed by atoms in the ground state.
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 590 nm590\textrm{ nm}
  2. 1.06 μm1.06\textrm{ }\mu\textrm{m}

Solution video

OpenStax College Physics for AP® Courses, Chapter 30, Problem 34 (Problems & Exercises)

OpenStax College Physics, Chapter 30, Problem 34 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 30, Problem 34 (PE) calculator screenshot 1
Video Transcript
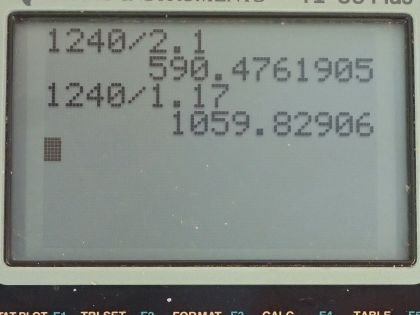
This is College Physics Answers with Shaun Dychko. This is an energy level diagram for neodymium and question (a) is asking what wavelength of light would be needed to stimulate an electron from the ground state up into this group that's above the metastable state? So this difference in energy is 2.1 electron volts. So we'll use this formula which says the energy of a photon is Planck's constant times speed of light divided by the wavelength and we will multiply both sides by λ over energy to solve for the wavelength needed and hc is 1240 electron volt nanometers and we will divide that by the energy of the photon, which is 2.1 electron volts and that will work out to 590 nanometers. So a photon that's incident with this wavelength— 590 nanometers— is capable of stimulating an electron from the ground state up into this group up here because all the photon energy will be absorbed by the electron and thereby increase the electron's energy. Okay! Part (b) says verify that the transition from the metastable second state to the first state results in a photon with a wavelength of 1.06 micrometers. So we'll use the same formula for the wavelength so that's 1240 electron volt nanometers divided by 1.17 electron volts and that is 1059.8 nanometers which we then convert into micrometers and sure enough, it's 1.06 micrometers.