Question
(a) Calculate the force the woman in Figure 7.46 exerts to do a push-up at constant speed, taking all data to be known to three digits. (b) How much work does she do if her center of mass rises 0.240 m? (c) What is her useful power output if she does 25 push-ups in 1 min? (Should work done lowering her body be included? See the discussion of useful work in Work, Energy, and Power in Humans.
Final Answer
- . This answer is open to discussion, and depends on your assumptions about the biomechanics involved during the recovery phase of the push-up. If the descent is seen as a resting phase with a negligible effort, then would be the best answer.
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 60 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
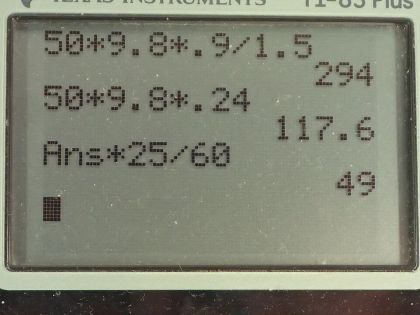
This is College Physics Answers with Shaun Dychko. This woman is doing a pushup and in part (a), we have to figure out what force is she applying on the ground which will be equal in magnitude to this reaction force applied on her due to the ground? And we are going to use the balancing of torques to figure that out— that's really a chapter 9 concept but anyway, it's needed here— because we can't say that the force she applies on the ground is half her weight... it might be tempting to say that because she has only two points of contact with the ground—her feet and her hands— but the center of gravity is not in the middle between these points and so the weight is not evenly distributed between her feet and her hands... more weight is going to be borne by her hands since the center of gravity is closer to her hands so this torque business takes that into account. So the lever arm for the reaction force multiplied by the reaction force is the counterclockwise torque and that counterclockwise torque has to equal the clockwise torque since she's moving at constant angular speed and so we have a clockwise torque due to the weight here and that's going to be the weight—mass times gravitational field strength— multiplied by the lever arm of the weight. So we divide both sides by the lever arm of the reaction force to solve for the reaction force. So that's mg times lever arm of the weight divided by lever arm of the reaction force and that's 50 kilograms times 9.8 Newtons per kilogram times 0.900 meters divided by 1.50 meters and that is 294 Newtons. Part (b) asks how much work does she do? Well that's going to be the change in potential energy of her body and we are told that her center of mass moves 0.240 meters upwards. So we take the weight 50 kilograms times 9.8 Newtons per kilogram multiply that by 0.240 meters and we get 118 joules of work done which is equal to her change in potential energy. Part (c) asks what is the power output? So that's going to be the work done divided by the time to do it. And so we are told she does 25 pushups in 60 seconds or 25 pushups in a minute, which we convert into 60 seconds by multiplying by 60 seconds per minute. So that's 117.6 joules of energy per pushup times 25 pushups and that's 49 watts. And we don't give much credit to the return stroke of the pushup... the processes in the muscle are very different coming down and you can feel that. When you come down, you are just balancing gravity and letting yourself fall and so there will be some work done... this power output calculation is not going to be perfect because it does not account for the small amount of work also done going down but that should be negligible compared to the work going up and so this is probably the closest we can realistically calculate.