Question
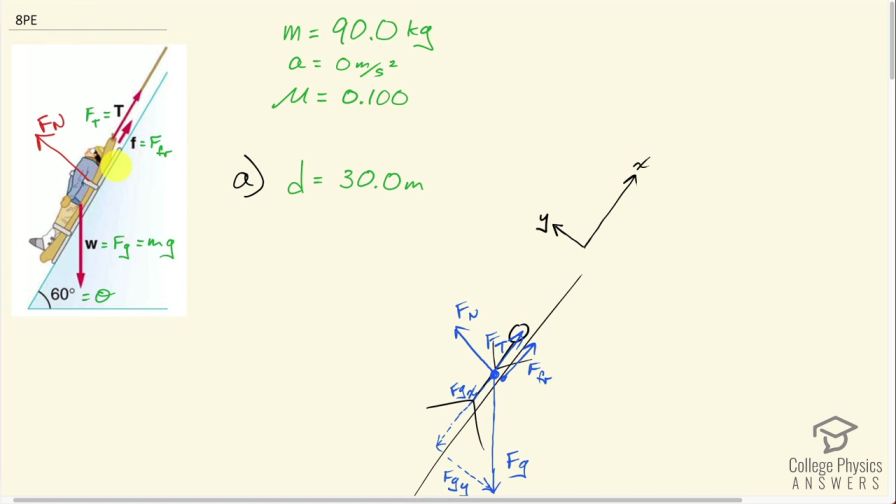
Suppose the ski patrol lowers a rescue sled and victim, having a total mass of 90.0 kg, down a slope at constant speed, as shown in Figure 7.37. The coefficient of friction between the sled and the snow is 0.100. (a) How much work is done by friction as the sled moves 30.0 m along the hill? (b) How much work is done by the rope on the sled in this distance? (c) What is the work done by the gravitational force on the sled? (d) What is the total work done?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 8 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
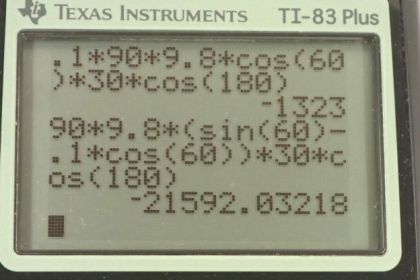
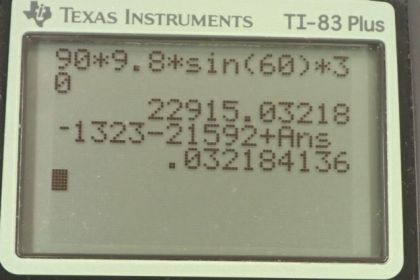
This is College Physics Answers with Shaun Dychko. This poor ski accident victim is being lowered down a snowy slope at constant speed, which means there's no acceleration, there's a tension force directed up the slope and also some friction directed up the slope as the skier is sliding down and there's a weight straight down and there's also a normal force perpendicular to the surface of the slope in this direction here. So there are a total of four forces on the skier and I have redrawn these forces over here where I have also done a little trick with our coordinate system and I have aligned the x-axis to be along the slope. You can choose any coordinate system you want in any question; conventionally, the coordinate system is y-axis straight up and x-axis positive to the right but in this question, it is more convenient for us to rotate our coordinate system so that we have x positive up the slope and y positive perpendicular to the slope. So we have the same four forces on this picture but I have drawn the components of gravity— the components that are parallel and perpendicular— to the coordinate system here... to the x-axis or to the slope. So we have gravity straight down still, this is no longer called the y-direction instead the y-direction is perpendicular to the slope so that means F g y here is negative because it's going the opposite direction that we have defined as positive— positive is up and to the left— and we have a component of gravity in the x-direction, which is down the slope and that's going to be negative as well. Okay! We know that the skier is going to travel 30.0 meters down the slope— we are told that in the question— and the mass of the skier and the sled is 90.0 kilograms, there's no acceleration which is another way of saying constant speed and the coefficient of kinetic friction between the sled and the snow is 0.100. Alright! So we always start our question by writing down the things that we know that we are given... I usually do that in green color. Alright! The slope is inclined at 60 degrees, with respect to horizontal, and in order to figure out the components of gravity here, we will need to figure out what the angles are in this triangle. So I am going to redraw this triangle off to the side a little bit... this triangle here I am going to redraw it with the slope angle here so that we can see which angle in the triangle corresponds to this angle of the slope. So imagine we have this slope here, we have gravity straight down like this and we know this angle here is θ— 60 degrees— and this is a right angle for sure because this is gravity straight down and the ground is horizontal and that makes this angle up here 90 minus θ because this angle in the top of this triangle plus θ have to total 90 since this angle here is 90 and the interior angles of a triangle have to total 180 so with 90 taken out by this right angle that leaves 90 left over for the sum of these two and so this one has to be 90 less than θ. Okay! So if we know that, it's 90 minus θ and that's this angle here that we just were talking about and this one is certainly 90 degrees because it's the angle between perpendicular components and that makes this angle here equal to θ because this one here is 90 minus θ and this angle has to be 90 minus that 90 minus θ which is 90 minus 90, which is 0, plus θ so in other words, this angle here is θ. Let's keep that in mind as we go forward and figure out components of gravity here. Okay! So consider the y-direction first. We know that the normal force in the positive y-direction is equal to the total forces in the negative y-direction of which there's only one... there's only the component of gravity that is directed in the negative y-direction and those are the only two things we have to think about in the y-direction. So the normal force is positive and then the y-component of gravity is in the minus direction and I like to put that minus explicitly in a formula and that totals 0 because there is no acceleration, it totals mass times acceleration in the y-direction because this is the net force in the y-direction but there's no acceleration so that's why there's a 0 there. And we can also say that the y-component of gravity is the weight mg times cos θ because this y-component is the adjacent leg of this gravity triangle and to find the adjacent leg, we multiply cosine of the angle by the hypotenuse so that's what we are doing here— the hypotenuse is mg. Okay! So we substitute that in place of F g y— that's what I have shown here in red— and that's all we can do for the y-direction. So then we turn our attention to the x-direction and we say that this friction force that is directed up the slope has to equal the normal force times the coefficient of friction. And so then we can create an expression for normal force now by dividing both sides by μ and then switch the sides around and we get normal force then is friction force divided by μ and we can substitute that in place of normal force in the y-direction formula, which is what we do here. And now we can add mgcos θ to both sides and then multiply both sides by μ and we end up with μmgcos θ is the force of friction. By the way, I don't think I made this clear in the beginning but the point of this question in part (a) is to figure out the work done by friction and so the work done is the force multiplied by the parallel component of the displacement and then that's going to be the distance, which is 30 meters, times cosine of the angle between the displacement and the friction force. But the angle is 180 degrees because the friction is directed up the slope and the displacement is down the slope and so the angle between them is 180 and that cos of 180 is what's going to give us our negative sign in our answer here. So the friction force—we did all this work to figure out what it is— and it's μmgcos θ so we substitute that in and we multiply that by d times cos of α and then we have an expression now that we can evaluate for the work done by friction. So it's 0.100—which is the coefficient of friction—times 90.0 kilograms—mass— times 9.80 Newtons per kilogram— gravitational field strength— times cos of 60 degrees— angle of the slope— times 30.0 meters times cos 180 and this is negative 1320 joules is the work done by friction. We expected a negative answer because the direction of the force is in the opposite direction to the displacement. Okay! So part (b) asks how much work is done by the rope on the sled in this distance? Alright! So to answer that we need to figure out what is the tension force and here's an expression for the x-direction which says that the friction force directed up the slope plus the tension force directed up the slope minus the component of gravity down the slope equals 0 because there's no acceleration in the x-direction. And we know that the component of gravity in the x-direction is F g times sin θ because this F g x is the opposite leg of this triangle and so we multiply the hypotenuse, which is mg, times sin of this angle θ. Alright! So that's where mgsin θ comes from— that's F g x and we substitute that in place of F g x here and then we can create an expression for the tension force by adding mgsin θ to both sides and also subtracting the friction force from both sides and so we get this expression here. And in part (a) we found an expression for the friction force—μmgcos θ— so we are going to substitute that part in now so we replace friction force with μmgcos θ factor out the common factor mg. So we have mg times (sin θ minus μcos θ)... looks kinda strange but there it is... that's the tension force! Okay! So the work done by tension will be the tension force multiplied by the component of the displacement parallel to the tension force. So that's mg (sin θ minus μcos θ) times the distance d times cos of the angle between the tension and the displacement, which again is going to be 180 degrees just as it was for the friction force because tension and friction are directed in the same direction. Okay! So we have 90.0 kilograms times 9.80 Newtons per kilogram times sin of 60 minus 0.100 times cos 60 times 30.0 meters times cos 180 and that is negative 2.16 times 10 to the 4 joules— that is the work done by the tension force. And lastly, what's the work done by gravity? So that's going to be the component of gravity parallel to the displacement. So that's mgsin θ times the distance times cosine of the angle between that component of gravity and the displacement. So that's 90.0 kilograms times 9.8 Newtons per kilogram times sin of 60.0 times 30.0 meters times cos of 0 degrees this time because they are in the same direction— the x-component of gravity and the displacement are both directed down the ramp— and so this works out to 2.29 times 10 to the 4 joules. And part (d) asks us for the net work done. We know what to expect here because net work is the change in kinetic energy and that's generally true and the word 'generally' means it's true in many different circumstances including when there are non-conservative forces involved such as friction. So it's one of these formulas that works in the real world and we expect the net work to be 0 because there is no change in kinetic energy of this person— they are being lowered at constant speed so they have kinetic energy but there's no change in the kinetic energy— but you know, we will bear this out by actually substituting in the values that we have calculated and confirm that it's true. So the work done by friction is negative 1323 joules minus the work done by the tension force 21592 joules plus 22915 joules work done by gravity and this all works out to 0.0 and there we go!