OpenStax College Physics for AP® Courses, Chapter 17, Problem 70 (Problems & Exercises)

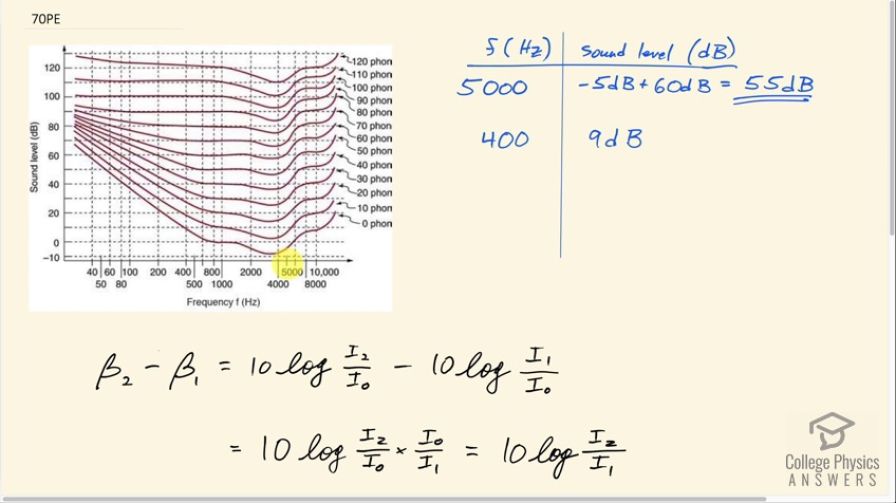
This is College Physics Answers with Shaun Dychko. A child has some hearing loss that affects only the frequency of around 5000 hertz and the hearing loss is 60 decibel hearing loss which means this threshold of hearing needs to be moved up 60 decibels and that is the threshold of hearing for this particular child so this zero phons wouldn't actually be up here at 55 decibels which is here. And so this zero phons line for this child would follow the usual curve because the child has normal hearing at other frequencies and then have a sharp rise here and then back down probably for the rest of it. Well, he or she would back down to where normal hearing is like that. Okay! So the question is how much more intense is a 5000 hertz barely audible sound compared to a 400 hertz barely audible sound? So we need to know what the decibel levels of those two sounds are. So zero phons means barely audible and the decibel sound level for 400 hertz is about 9 decibels because this point here crosses just under the dotted line and so that's about 9 decibels. And for 5000 hertz, the decibel level for normal hearing would be about negative 5 decibels and with a 60 decibel hearing loss that makes a total of 55 decibels for barely hearing 5000 hertz. So then we'll do some work here to figure out what the ratio of intensities are based on the difference in the sound levels. So sound level number 2 which is at 5000 hertz minus the sound level at frequency 1 which is 400 hertz is gonna be 10 times log of I 2 over I naught minus 10 times log of I 1 over I naught— these are the intensities in watts per square meter for the two sounds and this is the intensity at the threshold of hearing for normal hearing. So we can factor out the 10 and then we are left with... (maybe I'll show that step) and we are left with 10 times logarithm of I 2 over I 1 minus logarithm of I 1 over I naught (sorry that's a mistake there, it's I naught I should say) so log of I 2 over I naught minus log of I 1 over I naught. Now when you are taking the difference of two logarithms, you can instead take a single logarithm of the first argument divided by the second argument. So that's I 2 over I naught divided by I 1 over I naught but instead of dividing a fraction by a fraction, I prefer instead to multiply by the reciprocal of the denominator so this is gonna be I 2 over I naught multiplied by this flipped over I naught over I 1 and the I naught's cancel and we are left with 10 times log of I 2 over I 1. Now we are trying to solve for this I 2 over I 1 so let's do that by first dividing both sides by 10 and then switching the sides around and so we have logarithm of I 2 over I 1 equals β 2 minus β 1 over 10. Then we make both sides exponents for 10 and on the left side, we'll end up with I 2 over I 1 since the logarithm tells you what exponent the base of the logarithm— which if it's not written we assume is 10— it tells you what exponent the base needs in order to equal the argument. So if the base is 10 then the logarithm will tell you what exponent 10 needs in order to make I 2 over I 1 and so if then you make that the exponent for 10 sure enough you will get I 2 over I 1. Now on the right hand side, we have 10 to the power of sound level 2 minus sound level 1 over 10. So that's 10 to the power of 55 decibels minus 9 decibels all over 10 and this works out to 4.0 times 10 to the 4 is the ratio of these intensities.