OpenStax College Physics for AP® Courses, Chapter 17, Problem 10 (Problems & Exercises)

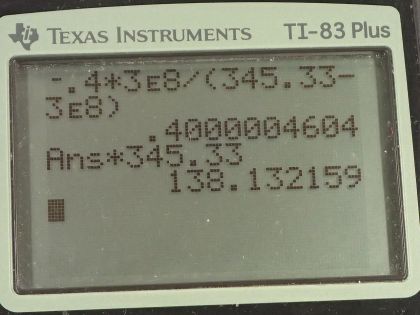
This is College Physics Answers with Shaun Dychko. A physicist measures the amount of time it takes for the sound from lightning to reach him as 0.400 seconds and the temperature of the air is 24.0 degrees Celsius which we convert into Kelvin by adding 273.15 and so the distance in the simple case where we ignore the time it takes for the light to get from the position of the lightning to the position of the physicist is just gonna be the speed of sound multiplied by the time the physicist measures but this time that they measure is going to begin after the light has arrived at the physicist but we ignore that light time until part (b). So in this part, the speed of sound is 331 meters per second times the square root of the absolute temperature divided by 273 Kelvin so that's 331 meters per second times square root 297.15 Kelvin divided by 273 which is 345.330 meters per second so we multiply that speed by 0.400 seconds to get a distance of 138 meters. And I kept lots of decimal places here in order to compare with the case in part (b) where we do consider the time it takes for light to get from the position of the lightning to the position of the physicist. So the distance between the physicist and the lightning bolt is some distance d and that distance will equal the speed of sound multiplied by the time it takes for the sound to travel which is not 0.400 seconds now in part (b) anymore; this 0.400 seconds is now considered to be the time difference between the time it takes for the sound to travel versus the time it takes for the light to travel. So the same distance could also be expressed as the speed of light multiplied by the time it takes for the light to travel. Okay! So this 0.400 seconds is the time the physicist measures because they begin their stopwatch after the light has been perceived. Okay! So this is a system of equations with three unknowns: we don't know t s, t l and we don't know d and so we are going to solve it by figuring out what the time for the sound to travel is and then use that to figure out d by multiplying it by the speed of sound. We'll begin by eliminating the variable d by subtracting equation 2 from equation 1 which will give us an equation that we'll call number 4. So the left hand side will make zero because it's d minus d and the right hand side will be v s times t s minus c times t l. Then we'll consider equation 3 and rearrange it to solve for t l and so we are adding t l to both sides and then subtracting 0.400 from both sides and we get t l equals t s minus 0.400 seconds. So this is something we can substitute into equation 4 to eliminate the variable t l and we do that substitution here in red. So this is equation 4, you know, version (b) you could say so zero equals v st s minus c times t s minus 0.400 seconds. So we distribute the speed of sound factor into the brackets here and we get v st s minus ct s plus because this minus and this minus make plus 0.400 times c; factor out the t s from these two terms then subtract this from both sides and divide both sides by this factor multiplying by the t s and then you get the time for the sound then is negative 0.400 seconds times c divided by v s minus c. So that's 0.400 times 3.00 times 10 to the 8 meters per second divided by 345.330 meters per second— speed of sound— minus 3.00 times 10 to the 8 meters per second and this gives 0.400000460 seconds; keeping lots of digits here in order to distinguish the distances in part (b) versus (a). So we have the speed of sound multiplied by this time for the sound to travel which is still 138 meters to the three significant figures that are appropriate considering the precision of measurement has three significant figures. But just to illustrate differences between the two scenarios where you consider the speed of light or not... when you do consider the speed of light is slightly greater distance minus the distance calculated when ignoring the time for the light to travel, this gives a percent difference of 0.000065 percent. So that means it's perfectly reasonable to ignore the time it takes for the light to travel because it's so fast.