Question
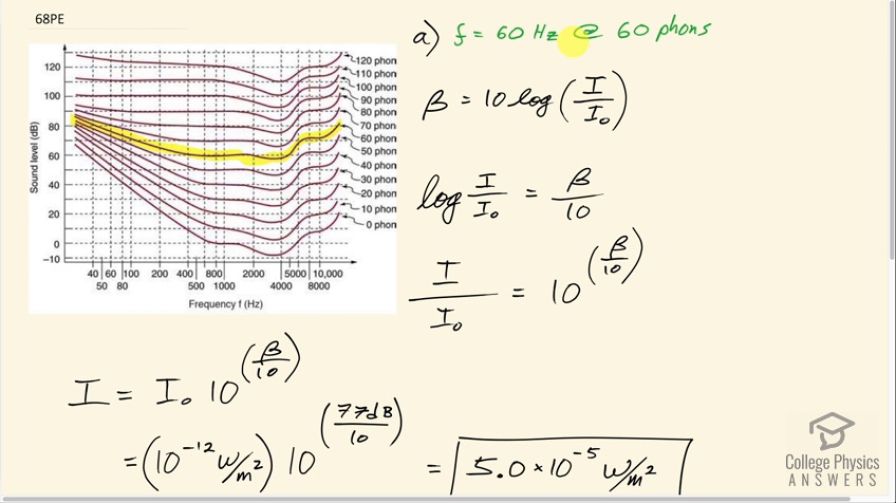
(a) Find the intensity in watts per meter squared of a 60.0-Hz sound having a loudness of 60 phons. (b) Find the intensity in watts per meter squared of a 10,000-Hz sound having a loudness of 60 phons.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 17, Problem 68 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Given a frequency of 60 hertz and a loudness level of 60 phons, what is the intensity of the sound in watts per square meter? Well if we knew what the sound level was in decibels, we could rearrange this to solve for the sound intensity I and so we'll do that by dividing both sides by 10 and then we get log of I over I naught equals the sound level over 10. and then make both sides exponents for 10 in which case, the left side becomes I over I naught because the logarithm tells you what exponent the base needs and the base if it's not written, we assume is 10 so the logarithm tells you what exponent 10 needs in order to equal this argument this I over I naught and so then if you take this whole exponent and put it on 10 then you will get this argument I over I naught. On the right hand side, we just have 10 to the power of sound level over 10. Then we can multiply both sides by I naught to solve for I. Okay! So we have now intensity in watts per square meter in terms of the reference or sorry... threshold of hearing intensity as well as the sound level. So we have to figure out the sound level now using this graph. So at 60 hertz, we can draw a line that's vertical and then see where it crosses the graph... the 60 phons line which I have highlighted in yellow here— this is the 60 phons curve— and where does it intersect that curve and what is the vertical coordinate of that intersection point? So where it intersects, we have to draw a line that's horizontal and see where it crosses the vertical axis and that looks like it's about 77 decibels... you know, this line here that's not labeled is 70 and it's a bit further than halfway between 70 and 80 so it's more than 75 let's call it 77. So the sound level is 77 decibels. So the threshold of hearing intensity is 10 to the minus 12 watts per square meter; we multiply that by 10 to the 77 decibels over 10, this works out to 5.0 times 10 to the minus 5 watts per square meter. In part (b), we are told that the frequency is now 10000 hertz and it's still 60 phons and we can use the same formula and our job with the graph then is to figure out what is the sound level at 10000 hertz and 60 phons loudness. So make a line that's vertical at 10000 hertz see where it crosses the 60 phons line and that's slightly above this dotted line here so slightly above 70... let's call it 72. So 10 to the minus 12 watts per square meter times 10 to the 72 over 10 is 1.6 times 10 to the minus 5 watts per square meter.
