Question
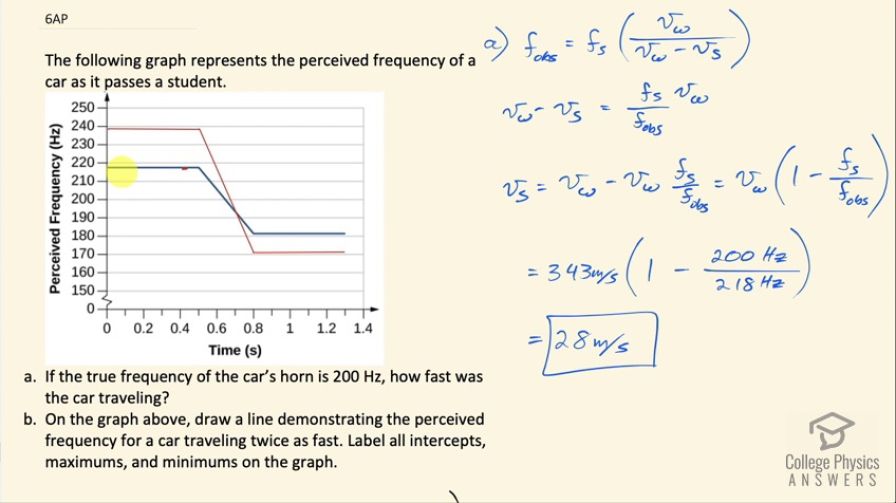
The following graph represents the perceived frequency of a car as it passes a student.
- If the true frequency of the car’s horn is 200 Hz, how fast was the car traveling?
- On the graph above, draw a line demonstrating the perceived frequency for a car traveling twice as fast. Label all intercepts, maximums, and minimums on the graph.
Final Answer
- ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 17, Problem 6 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
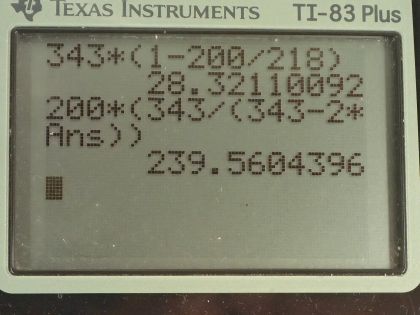
This is College Physics Answers with Shaun Dychko. A stationary student on the side of the road is observing the frequency of a car horn that's approaching and we are told that the car horn has a true frequency of 200 hertz but the student perceives about 218 hertz, which means the car must be coming towards them and then the car passes them and then well, the car is moving away from the student the Doppler shifted car horn frequency is about 181 hertz or so. So the first question in part (a) is to figure out how fast is the car traveling based on this observed frequency. So let's consider the moment where the car is approaching the student and in that case, we have a minus sign here where you have the observer is stationary and the source is approaching the observer— we have a minus sign in our Doppler shift formula— and we have the true frequency of the car horn— that's the frequency of the source— multiplied by the velocity of the wave involved, which is a sound wave and so in other words, this is the speed of sound divided by speed of sound minus the speed of the source, our job is to do some algebra to solve for v s. We'll start by multiplying both sides by v w minus v s divided by f obs and I am multiplying both sides of the equation by that and on the left side, we have v w minus v s and on the right side, we have f s times v w divided by f obs and then add v s to both sides and then subtract f s over f obs times v w from both sides and then switch the sides around and we have the speed of the source then is the speed of the wave minus the speed of the wave times frequency of the source divided by frequency observed and we can factor this v w out from both terms and so we have v w times 1 minus v s over f observed or f s I should say over f obs. Okay! So the speed of sound in air is typically 343 meters per second and we multiply that by 1 minus 200 hertz— true frequency of the car horn— divided by 218 hertz—their frequency observed— and the speed of this car must be 28 meters per second. And then we are meant to draw another line in this graph demonstrating the perceived frequency if the car was traveling twice as fast. So we are gonna label the maximums and the minimums and the maximum occurs at about 200 hertz times 343 divided by 343 minus 2 times the speed we found in part (a), this works out to 239.6 hertz. So at about just less than 240, we have our frequency when the car's approaching. And then when the car is going away from the student, we have a plus sign in our Doppler shift formula and so all the other numbers are otherwise the same so 200 hertz times 343 divided by 343 plus 2 times the speed of the car and this is 171.7 hertz and so we have about 171 here for the Doppler shifted frequency when the car is going away from the student.