Question
(a) Find the length of an organ pipe closed at one end that produces a fundamental frequency of 256 Hz when air temperature is . (b) What is its fundamental frequency at ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 17, Problem 48 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
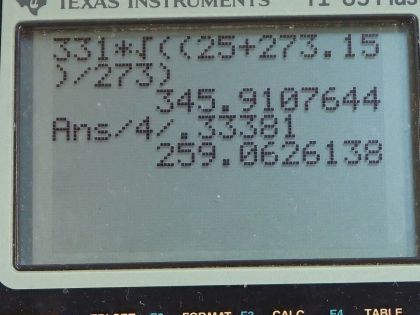
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An organ pipe which is modeled as a tube that's closed at one end has a fundamental frequency of 256 hertz when the temperature is 18.0 degrees Celsius which we convert into Kelvin by adding 273.15. The question in part (a) is to figure out what is the length of the organ pipe? So the nth harmonic is this number n which is natural numbers that are odd— 1, 3, 5, 7 and so on— multiplied by the speed of sound divided by 4 times the length of the tube. This means f 1 the fundamental is the number 1 substituted for the letter n times v over 4L and we can solve for L— the length of the tube— by multiplying both sides by L over f 1. So this makes the length equal to the speed of sound divided by 4 times the fundamental frequency. Now the speed of sound is something we have to calculate based on knowing the temperature is 18.0 degrees Celsius. So the formula for that is 331 meters per second times the square root of the absolute temperature divided by 273. So the absolute temperature is 291.15 Kelvin we divide that by 273, take the square root of that quotient, multiply by 331 and we get 341.826 meters per second. So we take that speed, divide it by 4 times the fundamental frequency of 256 hertz and we get a length of 0.334 meters. Part (b) asks what would the fundamental frequency be if the temperature changed to 25.0 degrees Celsius? So the length of the organ pipe is gonna stay the same but the speed of sound is gonna change as a result of this higher temperature. So we find the new speed of sound— call it v prime— and it's gonna be 331 meters per second times square root of 25.0 degrees Celsius plus 273.15 divided by 273 and so the speed of sound now is 345.911 meters per second. So this new fundamental frequency, we'll call it f 1 prime, equals the new speed of sound v prime divided by 4 times the length we found in part (a). So that's 345.911 meters per second divided by 4 times 0.33381 meters which is 259 hertz and this is actually a significant change! This would result in a different tuning for the orchestra that might be surrounding or playing with the organ because that's a difference in 3 hertz for the frequency of this organ pipe.