OpenStax College Physics for AP® Courses, Chapter 21, Problem 52 (Problems & Exercises)

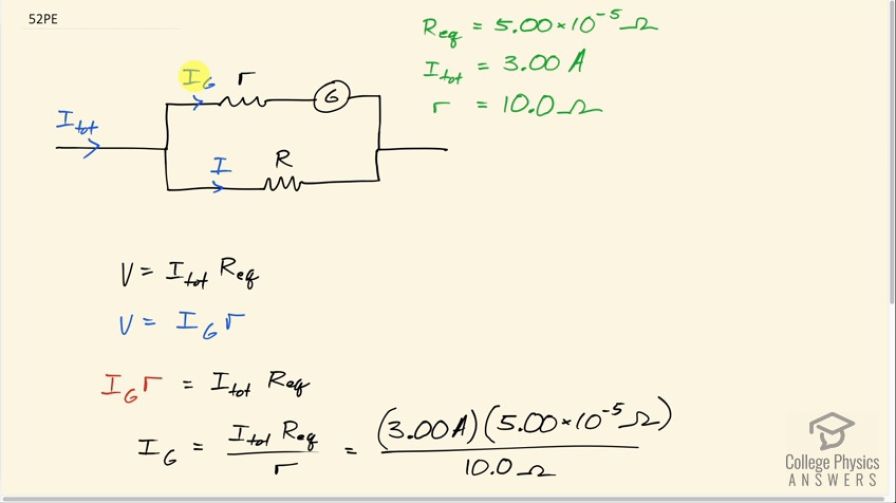
This is College Physics Answers with Shaun Dychko. In this question we want to know the sensitivity of the galvanometer that is to say what is this current through the galvanometer when there's a full scale reading? So the total resistance of this ammeter is 5.00 times 10 to the minus 5 ohms that's the equivalent resistance of this internal resistance of the galvanometer combined with its parallel shunt resistance here. The internal resistance of the galvanometer is 10.0 ohms so this is 10.0 ohms here and the total current being measured here is 3.00 amps— that's the total current going into this junction. So the voltage across the top branch here is the voltage across this whole thing is the total current multiplied by the equivalent resistance and you could also say that this is the current through the galvanometer multiplied by the internal resistance of the galvanometer because the voltage between here and here is the same as the voltage between here and here which is the same as the total voltage from here to there because all those corresponding points are parallel. Okay! So we can equate these two then and say the galvanometer current multiplied by the internal resistance of the galvanometer equals the total current given to us multiplied by the total resistance given to us and we divide both sides by the internal resistance of the galvanometer to solve for the current through the galvanometer when it has this full scale reading and that current is called the sensitivity of the galvanometer, the current that causes a full scale reading in other words. So that's 3.00 amps multiplied by 5.00 times 10 to the minus 5 ohms divided by 10.0 ohms—internal resistance— and that is 15 microamps.