OpenStax College Physics for AP® Courses, Chapter 21, Problem 2 (Problems & Exercises)

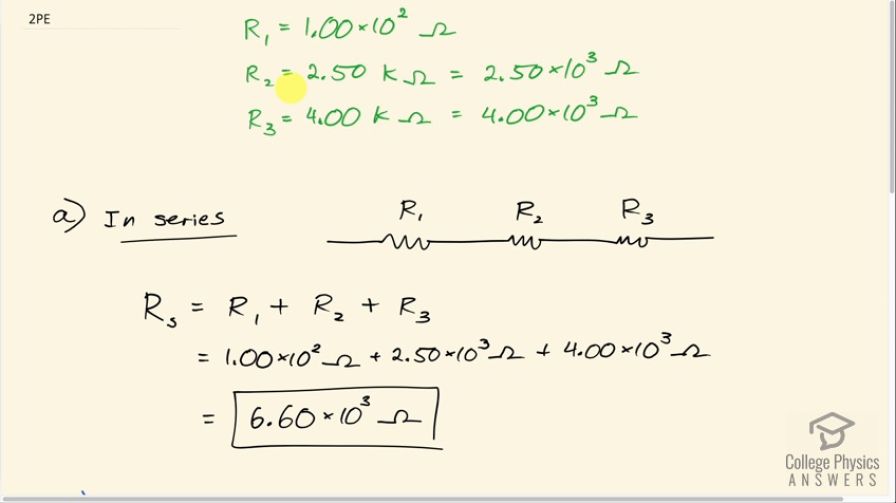
This is College Physics Answers with Shaun Dychko. We have three resistors: resistor one has a resistance of 1.00 times 10 to the 2 ohms; resistor two is 2.50 kiloohms and I write the prefix 'kilo' as times 10 to the 3; and then we have resistor three is 4.00 times 10 to the 3 ohms and it's useful to rewrite these prefixes as times 10 to the 3 because we want everything to be in the same units of ohms. In part (a) we are asked, what is the equivalent resistance of these three resistors in series? So series means it's one after the other and the total resistance is going to be the arithmetic sum— you just add them together of these three resistors. So we have 1.00 times 10 to the 2 plus 2.50 times 10 to the 3 plus 4.00 times 10 to the 3 ohms that gives 6.60 times 10 to the 3 ohms is... if we had one resistor and that resistance was equivalent to these three joined one after another, this one resistor that would be the equivalent resistance is 6.60 times 10 to the 3 ohms. Okay! In part (b) we are told put these three resistors in parallel, which means one end of each of the resistors is all connected together and then the other end of each of the three resistors is also connected together. So the current gets to choose which resistor it goes through whereas in series, the current was restricted only to one choice at a time— it had no choice, it had to go through one and then the other whereas in parallel, it can choose these three branches all at the same time. So the total parallel resistance is going to be the reciprocal of the sum of the reciprocals of each of the resistances. Now sometimes you see this formula written as... sometimes you see it as 1 over the parallel resistance equals 1 over R 1 plus 1 over R 2 plus 1 over R 3 and that's totally fine but then once you do this adding of the reciprocals, you have to take the reciprocal of your result to figure out what our parallel is and I am doing that by just putting all of this right hand side to the exponent negative 1 because that's what exponent negative 1 means is flip the number or take its reciprocal. Okay! And you will notice in the calculator screenshot, I am gonna write 1.00 times 10 to the 2 to the power of negative 1 instead of writing a fraction and you can do either way. So we have 1 over 1.00 times 10 to the 2 ohms plus 2.50 times 10 to the 3 to the power of negative 1 I am just saying that as a way to illustrate that you can, you know, talk about this as 1 over 2.50 times 10 to the 3 or you can talk about it as 2.50 times 10 to the 3 to the power of negative 1—either way is fine— plus 1 over 4.00 times 10 to the 3 ohms, take that sum and then raise it to the power of negative 1 and you get 93.9 ohms is the equivalent resistance when these three resistors are in parallel.