Question
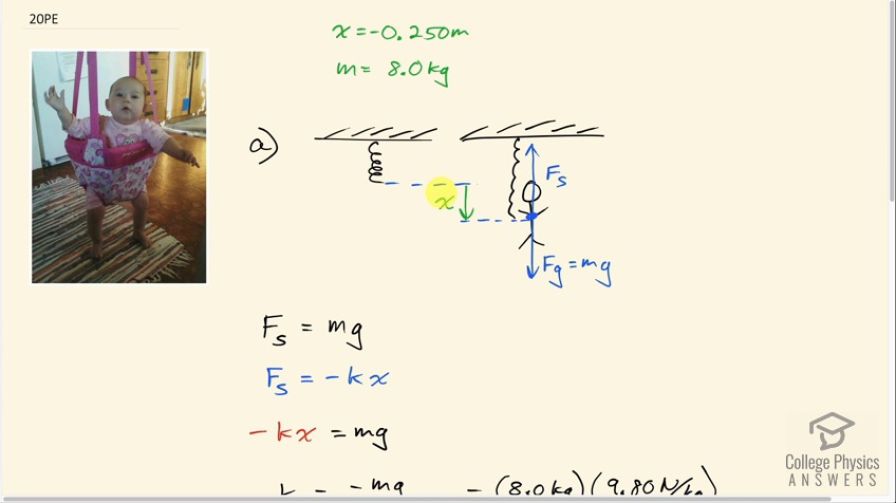
The device pictured in Figure 16.46 entertains infants while keeping them from wandering. The child bounces in a harness suspended from a door frame by a spring constant.
(a) If the spring stretches 0.250 m while supporting an 8.0-kg child, what is its spring constant?
(b) What is the time for one complete bounce of this child? (c) What is the child’s maximum velocity if the amplitude of her bounce is 0.200 m?
Final Answer
Solution video
OpenStax College Physics, Chapter 16, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. There's an 8.00 kilogram baby in a jelly jumper and the baby causes the spring to stretch by 0.250 meters. This stretch is in the downwards direction so we'll put a negative sign in front of that and we'll call it x because x is the letter used in this Hooke's law formula typically. So the force due to the spring is negative of the spring constant times the amount of stretching of the spring and the negative x and the negative sign of this formula will together make a positive which is good because positive is the upwards direction here we are assuming and the spring force is indeed upwards. It's balancing the force of gravity downwards, which is mg, and so because they are equal to each other, we can say negative kx equals mg and divide both sides by negative x and we get the formula for the spring constant: negative mg over x. So that's negative 8.0 kilograms times 9.80 newtons per kilogram divided by negative 0.250 meters which is 310 newtons per meter. Part (b) asks what is the time for one complete bounce of this child? So in other words, it's asking for the period— the time for one complete cycle. That is 2π times the square root of the mass of the child divided by the spring constant. So that's 2π times square root of 8.0 kilograms divided by 313.6 newtons per meter and that is 1.0 seconds. Part (c) asks for the maximum speed and that is square root of spring constant divided by mass multiplied by the maximum displacement from equilibrium which is also called the amplitude and that we are told is 0.200 meters. So we have square root of 313.6 newtons per meter—spring constant— divided by 8.0 kilograms times 0.200 meters and that's 1.3 meters per second is the maximum speed.
