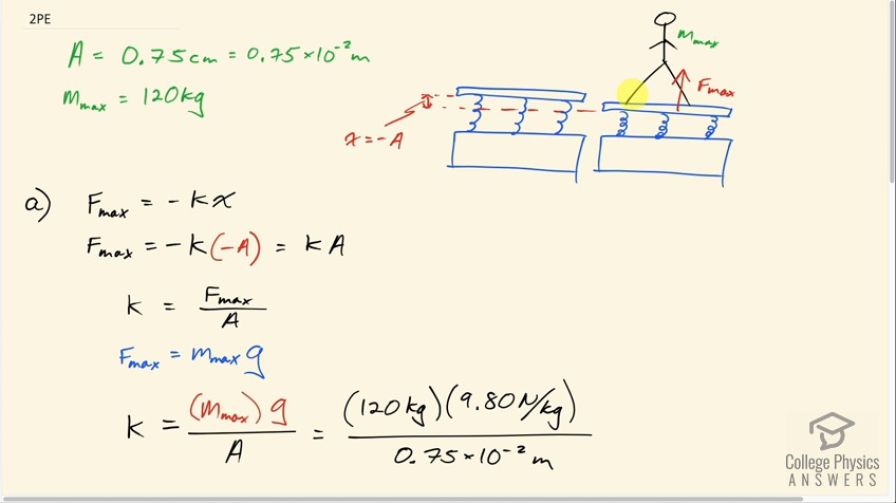
Question
It is weigh-in time for the local under-85-kg rugby team. The bathroom scale used to assess eligibility can be described by Hooke’s law and is depressed 0.75 cm by its maximum load of 120 kg. (a) What is the spring’s effective spring constant? (b) A player stands on the scales and depresses it by 0.48 cm. Is he eligible to play on this under-85 kg team?
Final Answer
- Yes, since 76.8 kg 85 kg, he can play on the under-85 team.
Solution video
OpenStax College Physics, Chapter 16, Problem 2 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A spring scale is used to measure the mass of these rugby players to see if they are eligible for the under-85 kilogram team. So when a player stands on this scale... if they have the maximum possible mass that the scale can handle then the scale will depress an amount equal to its amplitude— that's its maximum displacement from equilibrium, in other words— and it will get down to this height here and it will be exerting its maximum total force upwards. So the force that it exerts is the negative of its spring constant times its displacement from equilibrium and the maximum possible force will be that spring constant times negative of its amplitude. So the amplitude is the magnitude of its maximum displacement but here we are meant to put in x and so since this displacement x is downwards, we are taking up to the positive direction; this displacement downwards is equal to negative of the amplitude so we substitute negative A in place of x. This makes kA is the maximum force. Okay! And this is positive and it's directed upwards and so everything makes sense there... okay! So this amplitude is 0.75 centimeters, which is 0.75 times 10 to the minus 2 meters and the maximum possible mass is 120 kilograms. So we are gonna figure out the spring constant of the scale and that is the total effective spring constant of all the springs together and we can find it by dividing this by A and then this by A and say the spring constant equals the maximum force divided by the amplitude. Now the maximum force is the maximum mass times g because if this is in static equilibrium here, there's a force exerted downwards due to the player which is the force due to gravity on the player which is the player's mass, m max, times g and so the force upwards has to have the same magnitude. Okay! I'll make that positive there. Let's just label this diagram with magnitudes here. Okay! So we are going to substitute in m max times g in place of the maximum force and that means the spring constant is the maximum mass times the gravitational field strength divided by the amplitude of the scale. So that's 120 kilograms times 9.80 newtons per kilogram divided by 0.75 times 10 to the minus 2 meters which is 1.57 times 10 to the 5 newtons per meter is the spring constant. In part (b), it says that a player stands on the scales and depresses it by 0.48 centimeters; is he eligible to play on this under-85 kilogram team? So the force exerted by the scale is the negative of its spring constant times its displacement x and the force is gonna be equal to the mass of the player times g. So we substitute mg in place of F and then solve for m by dividing both sides by g and so we get that the mass is negative of the spring constant that we calculated in part (a) times this displacement which is downwards and so we put a negative in front of it. So negative 0.48 times 10 to the minus 2 meters divided by 9.80 newtons per kilogram and that is 76.8 kilograms. And so that means yes, this person can play on the under-85 team because their mass is less than 85.0 kilograms.
