Question
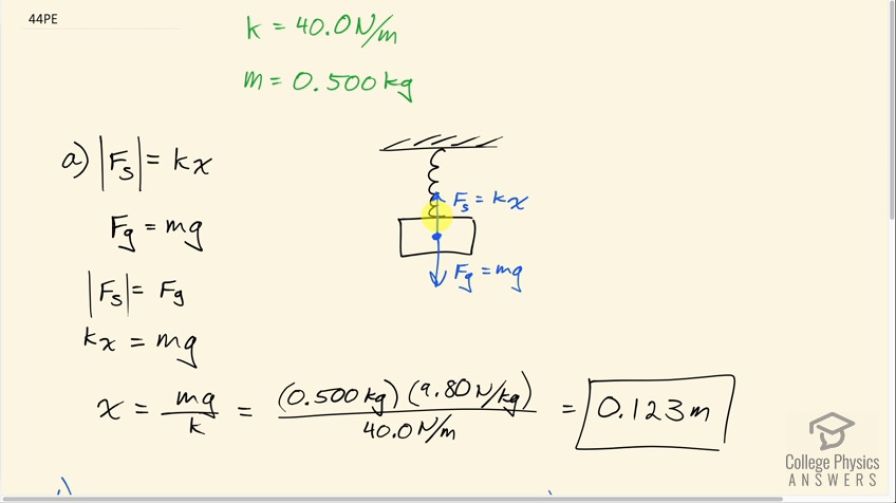
(a) How much will a spring that has a force constant of 40.0 N/m be stretched by an object with a mass of 0.500 kg when hung motionless from the spring? (b) Calculate the decrease in gravitational potential energy of the 0.500-kg object when it descends this distance. (c) Part of this gravitational energy goes into the spring. Calculate the energy stored in the spring by this stretch, and compare it with the gravitational potential energy. Explain where the rest of the energy might go.
Final Answer
- The energy stored in the spring is . As the spring is stretched internal friction within the spring material dissipates energy as heat.
Solution video
OpenStax College Physics, Chapter 16, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 0.50 kilogram mass is hanging from a spring with a spring constant of 40.0 newtons per meter; the mass is motionless which means it's sitting at its equilibrium position and the upwards spring force has to equal the downward force of gravity. So gravity is mg—mass times gravitational field strength— and the spring force has a magnitude of the spring constant multiplied by the amount of stretching x. Now just to avoid issues with negative signs, I'm taking the magnitude of this spring force— that's what these vertical bars are representing— and so that is spring constant times the amount of stretching and then the force of gravity is mg and these two are going to be equal to each other and so we can say kx equals mg. So that means x—the amount by which the spring is stretched— is mg divided by the spring constant. So that's 0.50 kilograms times 9.80 newtons per kilogram divided by 40.0 newtons per meter which is 0.123 meters. And then part (b) asks how much has the gravitational potential energy of this mass decreased due to change in positions from when the spring is at its equilibrium position versus when it's stretched. So the mass has fallen the amount by which the spring has stretched in other words. So that's 0.500 kilograms times gravitational field strength times the spring stretch and that is 0.600 joules. Now the potential energy stored in the spring when it is stretched is one-half times the spring constant times the amount of stretching squared. So that's one-half times 40.0 meters times 0.1225 meters squared which is 0.300 joules and this is less than the amount by which the mass has lost gravitational potential energy and the reason for that is that while the spring is being stretched, there is internal friction within the spring material that dissipates energy as heat and so we expect this potential energy stored in the spring to be less than the change in gravitational potential energy. So if there was no friction within the spring material, we would expect this to be the same as that. Okay!
