Question
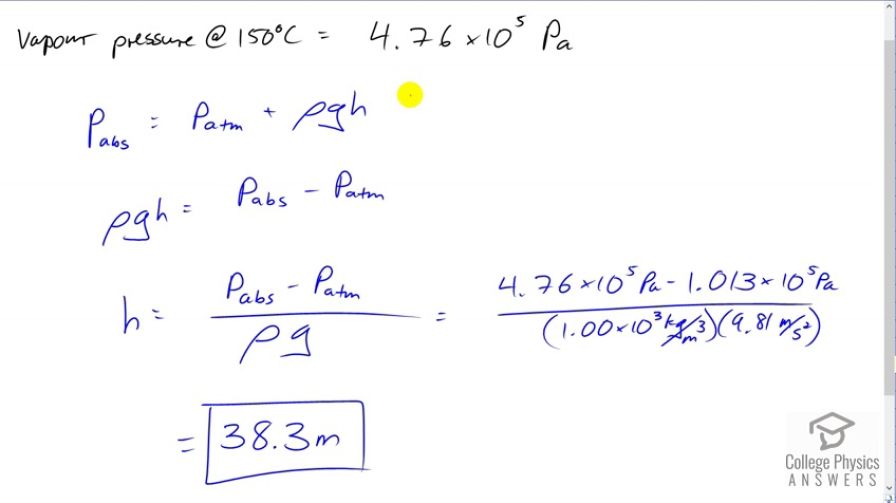
The boiling point of water increases with depth because pressure increases with depth. At what depth will fresh water have a boiling point of , if the surface of the water is at sea level?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 65 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
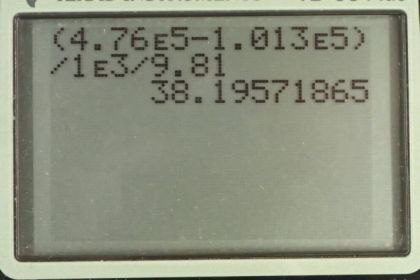
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the depth within fresh water at which point if you had a pot of water you could boil it at 150 degrees Celsius. So, the vapor pressure according to Table 13.5 at a 150 degrees Celsius is 4.76 times ten to the five pascals. And so we need to find a water depth that has this absolute pressure. Now, we're told that the surface of the water is at sea level, so that we know that the air above the water is contributing an amount pressure equal to this standard atmospheric pressure which is a pressure given at sea level. So, we know the absolute pressure, it has to be this vapor pressure. And we know this atmospheric pressure and we're going to be adding this pressure due to the column of water and we're going to find out what height the column should have. So, we'll subtract atmospheric pressure from both sides and that isolates rho gh on one side equals absolute pressure minus atmospheric pressure. And then we'll divide both sides by density of water and multiplied by the acceleration to the gravity. So, the height of the water column or the depth within the water in other words, is going to be the absolute pressure minus atmospheric pressure minus density of water times g. So that's 4.76 times ten to the five pascals minus 1.013 times ten to the five pascals divided by 1000 kilograms per cubic meter times 9.81 meters per seconds squared giving a depth of 38.3 meters.