Question
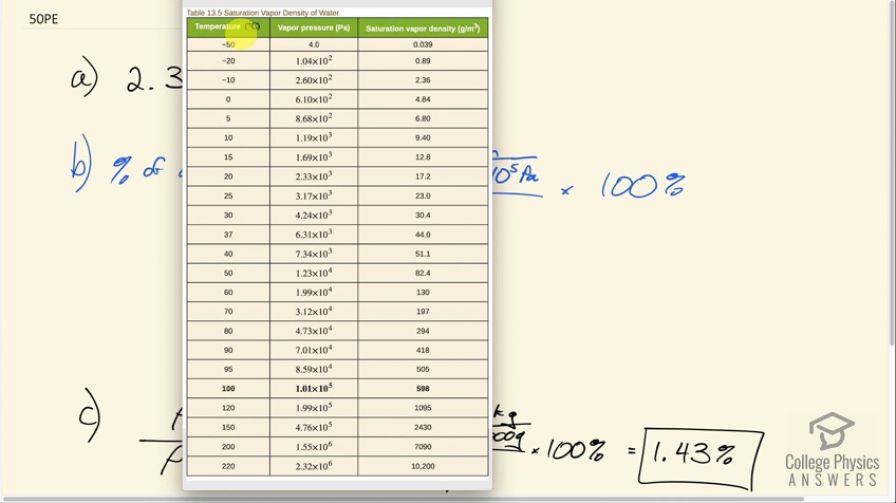
(a) What is the vapor pressure of water at ? (b) What percentage of atmospheric pressure does this correspond to? (c) What percent of air is water vapor if it has 100% relative humidity? (The density of dry air at is .)
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 50 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The vapor pressure of water at a certain temperature is something that we look up in table 13.5. So we follow the temperature column to 20 degrees Celsius and the vapor pressure is 2.33 times 10 to the three pascals. In part B we are asked: what percentage of atmospheric pressure does this correspond to? So we convert that vapor pressure into atmospheres by diving by 1.013 times to the five pascals and that's the pressure in units of atmospheres divided by one atmosphere times 100% is 2.30%. And in this part C we are finding what percentage this density of the water would be as a percentage of the density of dry air. Now this is just an approximation because this is not the density of the air at 20 degrees Celsius when it contains some water. This is the density of dry air. It's a bit more complicated to figure out what the total density is of the air plus water combined. So this strictly speaking is not the density of the water in the air. But anyway it's close enough. I mean, there are density calculators online and you can find that the density of air with some water in it at 20 degrees Celsius is about 1.19 which is pretty close to this. So, we have 17.2 grams per cubic meter at 20. Also that came from table 13.5 Then we convert that into kilograms per cubic meter in order to divide by the kilograms per cubic meter in the denominator. So that's 17.2 divided by a thousand divided by 1.2 kilograms per cubic meter and we get 1.43%.
