Question
In the text, it was shown that for gas at STP. (a) Show that this quantity is equivalent to , as stated. (b) About how many atoms are there in one (a cubic micrometer) at STP? (c) What does your answer to part (b) imply about the separation of atoms and molecules?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 27 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Prev
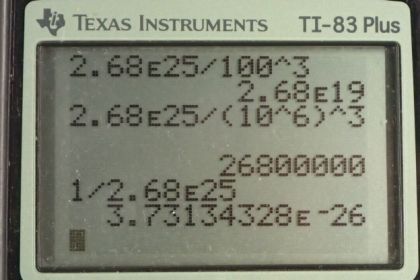
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. For gas at standard temperature and pressure, the number of atoms or molecules divided by the volume will be 2.68 times ten to the 25 particles per cubic meter. And if you want to convert this into per cubic centimeter, we'll multiply it by one meter for every hundred centimeters three times and this gives 2.68 times ten to the 19 per cubic meters. So there should be particles per cubic meter, but we don't have to write the word particles because it's not really a dimension, it's just a counting figure. Now, in one cubic micrometer, we're going to figure out how many atoms are present. And so we'll take the number of atoms per volume and multiply it by the volume. So, we have this 2.68 times ten to the 25 atoms per cubic meter which we convert into atoms per cubic micrometer by multiplying by one meter for every ten to the six micrometers three times and then multiply that by the volume of one cubic micrometer. And this gives 2.68 times ten to the seven atoms. And then we're going to figure out what volume does a single atom occupy. And then, we'll make an assumption that, that atom is occupying a cubic space here. And we'll find the side length to that cube. So, the volume of an atom is one cubic meter for every 2.68 times ten to the 25 atoms giving us 3.7313 times ten to the minus 26 cubic meters per atom. So we took the reciprocal of the figure that was given to us at the beginning of this question. And we'll assume that this volume is the side length of the cube cubed. And so we'll solve for L by taking the cube root of both sides here. So, the length volume occupied by atom which we don't really know whether it's the size of the atom or whether the separation between atoms and the reality is that it's some combination of the two. The atom will take up some amount of space here and the separation will be something less than what we're calculating here. But this L represents the separation plus diameter of the atom. So cube root of the volume occupied by an atom is cube root of 3.7313 times ten to the minus 26 cubic meters per atom giving us this millimeters occupied by a single atom in along one line. And this is 3.34 nanometers. So if the atom had no volume at all then this would be the separation between them. But since atoms do have some volume, the separation between them will be something less than this.
Comments
I was completely lost on what you were doing for part (c) until you actually stated the word “separation.” I did not understand why you were solving for all that until I realized what you were doing/how it related to the question.