Question
If you want to cook in water at , you need a pressure
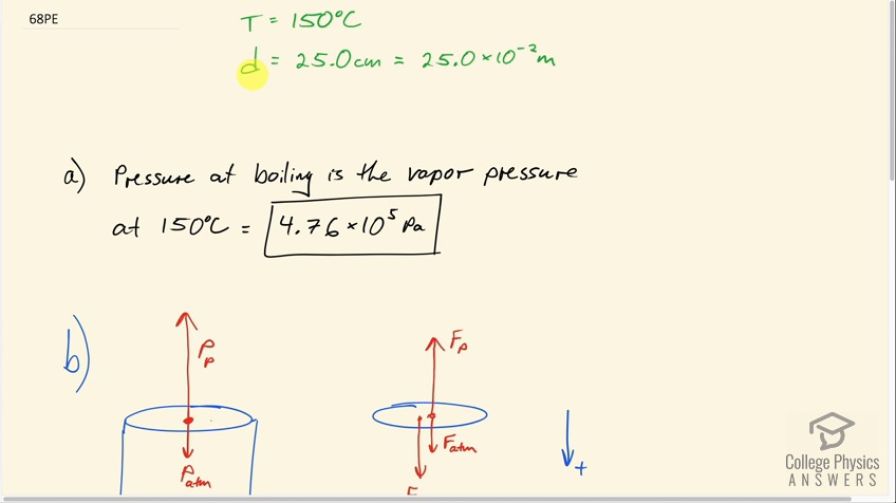
cooker that can withstand the necessary pressure. (a) What pressure is required for the boiling point of water to be this high? (b) If the lid of the pressure cooker is a disk 25.0 cm in diameter, what force must it be able to withstand at this pressure?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 68 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We want to use a pressure cooker that has water boiling at 150 degrees Celsius. And the diameter of the lid of the pressure cooker we're told is 25 centimeters. And as usual, we're writing down the stuff that we know. We'll do our unit conversions. We want to convert this into meters in order to have meters-kilograms- seconds-type units, MKS units. And the prefix center means multiply by 10 to the minus 2. So, Part A says given that the temperature for boiling of water is 150 degrees Celsius what is the pressure necessary? When the water is vapor pressure equals the pressure of the air above it, that's when boiling will occur. And so at 150 degrees Celsius, the vapor pressure - if we look it up in table 13.5 - at 150 degrees Celsius, the vapor pressure is four point seven six times 10 to the 5 pascals. And so that's going to be our answer. So this is the amount of pressure that's needed in their above the water in order to have boiling occur at this temperature. Part B says what force does the lid need to withstand in order to contain this pressure inside the pressure cooker? So there's a pressure due to the pressure cooker; I just labeled it p, subscript p, pushing outwards on the lid, and then there's the atmospheric pressure that's pushing down on the lid. And then if we draw a free body diagram of the lid, we have the force due to the pressure upwards, the force due to the atmosphere downwards and then also this force due to the lid downwards. And this force plus atmosphere force downwards in total has to equal the force due to the pressure upwards. I'm taking down to be positive just because I want to have a positive answer for the force due to the lid. So the force due to the lid plus the force due the atmosphere both positive downwards minus force due to the pressure inside - minus because it's in the negative direction which we're taking to be up unconventionally here, but that's just what I chose to do - and all that equals zero. And also I'm using magnitudes for these forces and putting their minuses and negatives and positives outside of the terms. Sometimes you'll see professors write pluses everywhere here. That's also fine so long as you have your negatives within the term. But I find that a bit confusing. I like to have all these numbers positive and just put the minuses outside of the term. So we'll add F P to both sides and subtract F A T M from both sides. And then we get force to the lid is the force due to the pressure inside the pressure cooker minus the force due to the atmosphere. So pressure is force per area - that's the definition and we can solve for force by multiplying both sides by A because our job is to is to take the pressures that we know and turn them into forces based on the area of this lid knowing that its diameter is 25 centimeters. So, force is pressure times area and for a circular lid then that area is going to be pi R squared and R is going to be half the diameter. And so we have pressure times pi times diameter squared divided by 4. So this gets substituted in for the force due to the pressure. Then they have the pressure due to the pressure cooker here. And then we have the same term but with the atmospheric pressure here. And this pi D squared over 4 can be factored out and multiply that by the difference in pressures. So basically the force due to the lid is the force due to the net pressure; so the amount by which these pressures differ. So that's pi times 25 times 10 to the minus 2 meters diameter squared divided by four, times four point seven six times 10 to the 5 Pascal's, minus atmospheric pressure gives a force of 1 point 84 times 10 to the 4 newtons.
