Question
Much of the gas near the Sun is atomic hydrogen. Its temperature would have to be for the average velocity, to equal the escape velocity from the Sun. What is that velocity?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Prev
Calculator Screenshots
Video Transcript
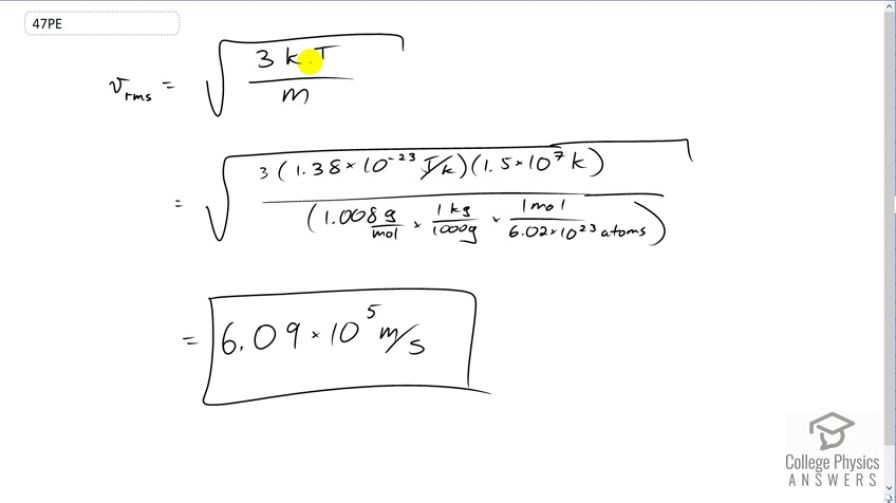
This is College Physics Answers with Shaun Dychko. We're given the temperature near the sun at which atomic hydrogen has the escape velocity of the sun. So we'll figure out what that escape velocity is by taking the square root of three times Boltzmann's constant times the temperature in Kelvin, divided by the mass in kilograms per atom. So we take the square root of three times 1.38 times ten to the minus twenty-three joules per Kelvin, Boltzmann's constant, times 1.5 times ten to the seven Kelvin, temperature near the sun, and divide by the mass of the hydrogen atom in kilograms. So we have 1.008 grams per mole that I looked up in Appendix A at the end of the textbook. Then multiply by one kilogram for every 1000 grams and then times by one mole for every 6.02 times ten to the twenty-three atoms, this is Avogadro's number, and then we end up with 6.09 times ten to the five meters per second must be the escape velocity of the sun.
Comments
where does the 6.02 x 10^23 atoms come from?