Question
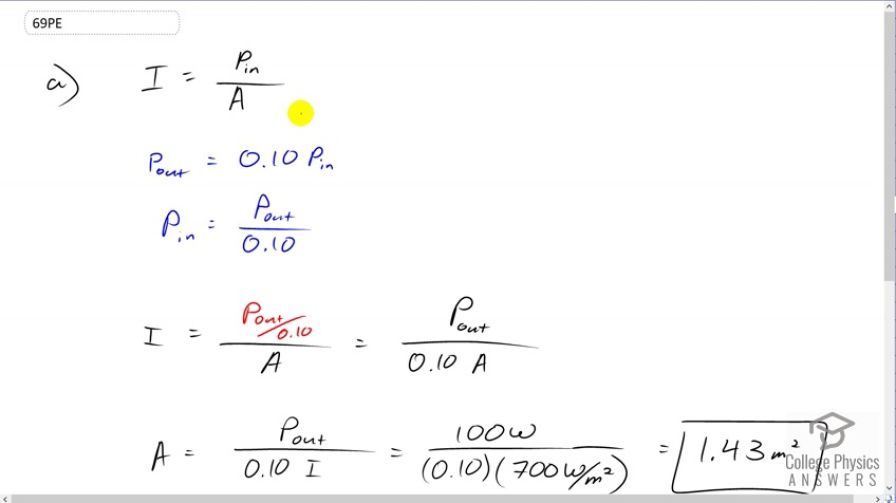
(a) A photovoltaic array of (solar cells) is 10.0% efficient in gathering solar energy and converting it to electricity. If the average intensity of sunlight on one day is what area should your array have to gather energy at the rate of 100 W? (b) What is the maximum cost of the array if it must pay for itself in two years of operation averaging 10.0 hours per day? Assume that it earns money at the rate of 9.00 ¢ per kilowatt-hour.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 16, Problem 69 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a photo-voltaic array of solar cells that is ten percent efficient and what area should the array have to gather energy at a rate of 100 Watts given that the intensity of the sun is 700 Watts per square meter? So intensity is the input power divided by area. The output power of the solar array is going to be ten percent or 0.1 times the input power. We can solve this for P in as P out divided by 0.1 and then we'll substitute that into this intensity formula. So intensity is P out over 0.1, all over area. Then we can multiply top and bottom by 0.1 and we get P out over 0.1 times A. We can solve for A by multiplying both sides by A and dividing both sides by intensity. We get A is P out divided by 0.1 times intensity. So it's 100 Watts divided by 0.1 times 700 Watts per square meter and this is 1.43 square meters must be the area of the solar array. Now the cost -- this is the amount of money that you make from the electricity generated by the array, and this will be the break-even cost of purchasing the array. So we have to go -- basically, we have to go power multiplied by time and then multiplied by this to get energy and then multiply by this cost per energy. The units are a bit funny though. To make numbers that are easier to work with, the units for this sort of calculation is chosen to be dollars per kilowatt hours. A typical electricity bill is written this way. So the energy unit is not Joules but it's kilowatt hours which is power multiplied by time but instead of Joules multiplied by -- sorry, instead of watts multiplied by seconds in order to get Joules we have kilowatts multiplied by hours to get kilowatt-hours. We have to convert our power in watts into kilowatts so we multiply by one kilowatt for every 1000 watts and this gives us kilowatts. Then we have to multiply by a time in units of hours. So we have ten hours per day and multiply by two years. So this gives us watt-years per day which is a very goofy unit and then multiply by 365 days per year gives us a time unit of hours. This is a power unit of kilowatts and so this together makes kilowatt-hours. That multiplied by 0.09 dollars per kilowatt hour is going to result in dollars. So we've 100 times ten times two times 365 times 0.09 gives us 65 dollars and 70 cents is the break-even cost of the array.
