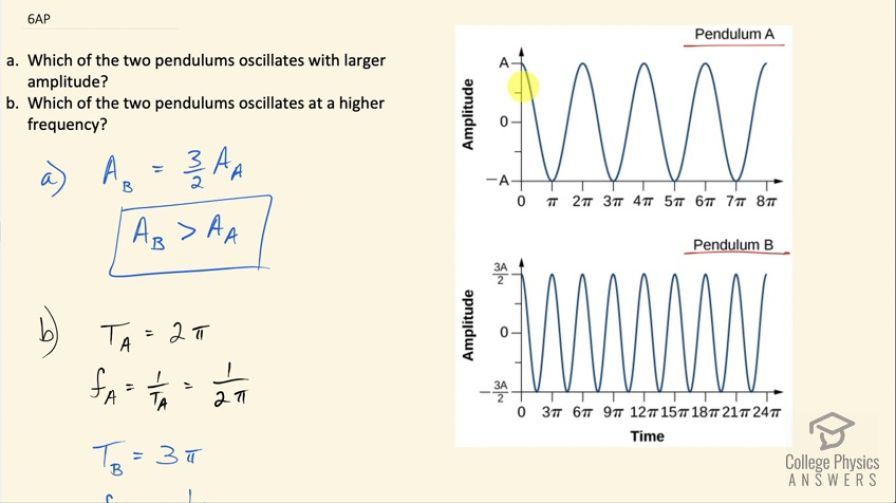
Question
Use these figures to answer the following questions.
- Which of the two pendulums oscillates with larger amplitude?
- Which of the two pendulums oscillates at a higher frequency?
Final Answer
- Pendulum B has a greater amplitude.
- Pendulum A has the greater frequency.
Solution video
OpenStax College Physics for AP® Courses, Chapter 16, Problem 6 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two graphs here: one for pendulum A and the other for pendulum B showing the amplitude versus time and time is measured in terms of π... multiples of π and the question in part (a) is which of the two pendulums oscillates with larger amplitude? And this pendulum has an amplitude of A so it reaches a displacement from equilibrium of amount A whereas this one reaches a displacement from equilibrium an amount 3 over 2A. So the amplitude of B is 3 over 2 times the amplitude of A and so this is the number 1.5 so the amplitude of pendulum B is greater than the amplitude of pendulum A. In part (b), it's asking which of the two pendulums oscillate at higher frequency? Well, it's easier to measure the period from this graph and so if we consider this maximum here and then the amount of time it takes to get to the next maximum here, this interval in time is 2π— it's starting from zero, ending at 2π— and so the frequency of pendulum A is the reciprocal of a period so that's 1 over 2π; the period for pendulum B, it starts here and then ends here at 3π and the frequency of B then is 1 over 3π and 1 over 2π is a bigger number than 1 over 3π because when you have the denominator of a quotient being smaller, the quotient becomes larger so the frequency of pendulum A is greater than the frequency of pendulum B. And you really have to do this math to see that because the graphs are made in such a way that it appears as though pendulum B has a greater frequency but it's because the horizontal scales are different; this physical distance here represents only an interval of π time whereas the same physical distance here represents a much greater time of 3π so you can't just visually look at the two, you have to do this calculation.