Question
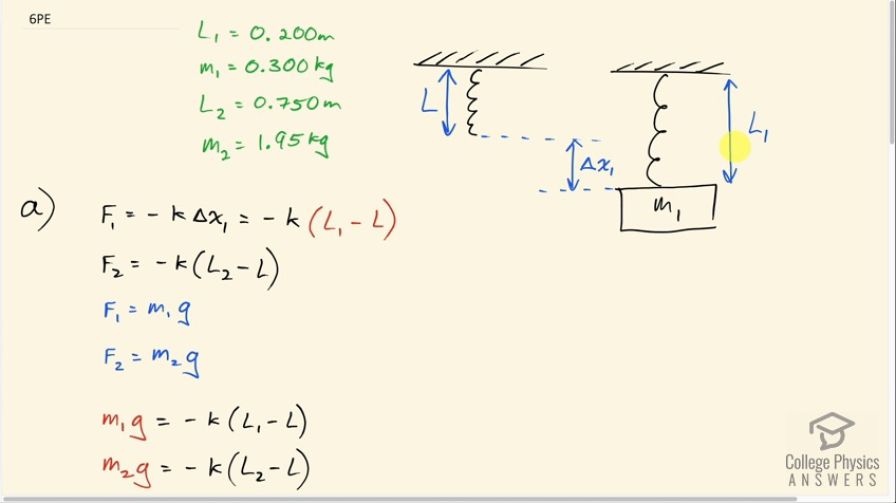
A spring has a length of 0.200 m when a 0.300-kg mass hangs from it, and a length of 0.750 m when a 1.95-kg mass hangs from it. (a) What is the force constant of the spring? (b) What is the unloaded length of the spring?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 16, Problem 6 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A mass, we'll call it m 1, is hanging from a spring and stretches it to a total length of L 1 and we are told that L 1 is 0.200 meters and I'll put a negative sign in front of this to indicate that this is towards the downwards direction and we are taking upwards to be positive. So the force that's going to be exerted upwards on this mass, F 1, is going to equal negative of the spring constant times the stretching of the spring which is this amount here compared to its equilibrium position when there's no mass hanging on it. And so Δx 1 is also negative— it's in this downward direction— and we don't know what it is and turns out that it doesn't matter... we just need to know what L 1 is— this total length— for mass m 1 and then we also need to know the total length for a second mass m 2. So F 1 then is this negative k times Δx 1 but Δx 1 is the difference between this total length L 1 minus this equilibrium length with no mass hanging on it; we'll call it just L. And so by the same logic, we have F 2 is negative k times this total length which would be L 2 given a mass 2 here so L 2 minus the same equilibrium length, L. And the force upwards in the first case is going to balance the gravity downwards which would be m 1 times g and F 2 will be m 2g and so we can substitute for each of these here and we have m 1g then is negative k times L 1 minus L and m 2g equals negative k times L 2 minus L. Okay! Now our job is to solve for k so we can subtract these two equations and so we have m 2g minus m 1g so that's subtracting the left sides. On the right hand side, we would have negative k times L 2 minus L minus negative k times L 1 minus L and this horizontal line with two tick marks here is just to say that copy this line here equals negative kL 2 plus kL— that's distributing this negative k into the brackets there— and then plus k times L 1 because negative times a negative makes a positive minus k times L because there's three negative's here to make total negative kL there and then the minus kL and the positive kL make zero and we can factor out the k among the two remaining terms and write (L 1 minus L 2). And then we have g factored out here so g times m 2 minus m 1 equals k times L 1 minus L 2 and then we solve for k by dividing both sides by L 1 minus L 2 and so k is g times m 2 minus m 1 over L 1 minus L 2. So that's 9.80 newtons per kilogram times 1.95 kilograms minus 0.300 kilograms divided by L 1 which is minus 0.200 meters minus L 2 which is negative 0.750 meters and this gives 29.4 newtons per meter is the spring constant. In part (b), we are asked to figure out what is this length when there's no mass hanging... the equilibrium length with no mass? So we'll say that F 1 is negative k times L 1 minus L as we said up here and that's equal to the weight of the mass that's hanging, m 1g, and we can distribute the k into the brackets so negative kL 1 plus k times L equals m 1g and we are gonna solve for L here. First we'll add kL 1 to both sides and then we have kL equals m 1g plus kL 1 and then divide both sides by k. So the length of no mass then is m 1g plus k times L 1 over k. So that's 0.300 kilograms times 9.80 newtons per kilogram plus the spring constant times the total length when the mass m 1 is hanging— negative 0.200 meters— all divided by the spring constant which gives negative 0.100 meters. Now asking for a length suggests looking for a positive answer or a magnitude and so we are just gonna make this positive and that's okay; first let's understand why it's negative. So L in our work down there is representing this position compared to you know x equals zero or I guess you could say y because we are talking about the vertical direction y equals zero here at the ceiling and this is L down here which is in the negative direction compared to zero. Okay! But we'll just take the magnitude of that position to get its length which is 0.100 meters.
