Question
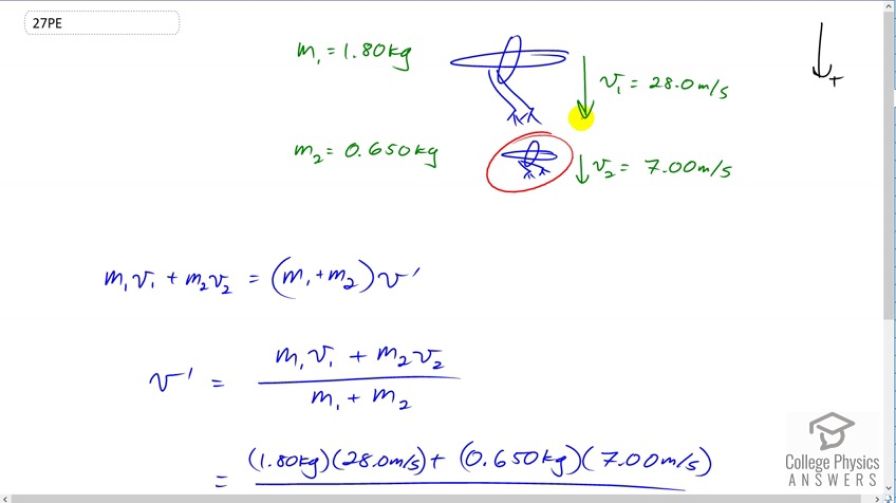
A 1.80-kg falcon catches a 0.650-kg dove from behind in midair. What is their velocity after impact if the falcon’s velocity is initially 28.0 m/s and the dove’s velocity is 7.00 m/s in the same direction?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 27 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 1.8 kilogram falcon is descending on to a 0.65 kilogram dove. The dove is trying to escape with a speed of seven meters per second down, but the falcon has a greater speed v one, 28.0 meters per second down and we're taking down to be the positive direction just for convenience. The question is once they stick together in this perfectly inelastic collision, what will the speed of this pair of birds be. So the momentum initially is the mass of the falcon times the velocity of the falcon, and then plus the mass of the dove times the velocity of the dove. That's going to equal their combined mass because they're going to become one object after they stick together, multiplied by their combined velocity v prime. Our job here is to solve for v prime. So we divide both sides by m one plus m two and then switch the sides around. We get v prime is the total momentum initially divided by the total masses after they stick together. So that's 1.8 kilograms mass of the falcon, times 28 meters per second, plus 0.65 kilograms, mass of the dove, times its initial speed of seven meters per second, divided by 1.8 kilograms plus 0.65 and that gives 22.4 meters per second will be the velocity after they stick together. It's positive and we've taken positive to be the downward direction, so this is 22.4 meters per second down.
