Question
Mass A (2.0 kg) is moving with an initial velocity of 15 m/s in the +x-direction, and it collides with mass B (4.0 kg), initially moving 7.0 m/s in the +x-direction. After the collision, the two objects stick together and move as one. What is the change in kinetic energy of the system as a result of the collision?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 44 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
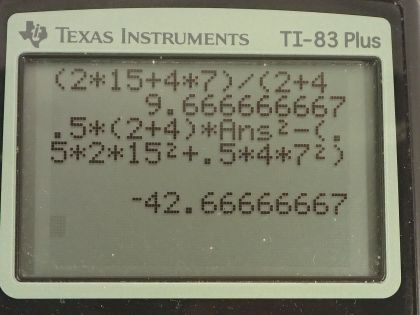
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Mass A, which is 2.0 kilograms, is moving in the positive x-direction with a speed of 15 meters per second and mass B is moving in the same direction with a speed of 7.0 meters per second and then after they collide because mass A is gonna catch up to mass B, we are told that they stick together and this combined mass will move with some velocity we'll call v prime and we have to figure out what the change in kinetic energy is and in order to know that, we need to know what this speed v prime is so let's use conservation of momentum to find v prime. So the total momentum before collision equals the total momentum after collision and before collision, we have mass A times its velocity plus mass B times the velocity of mass B and that's going to equal the combined mass of this object, which is m A plus m B multiplied by its speed v prime. We'll divide both sides by m A plus m B to solve for v prime and then switch the sides around as well so v prime is m Av A plus m Bv B divided by the total mass. So that's 2.0 kilograms times 15 meters per second plus 4.0 kilograms times 7.0 meters per second divided by the total mass of 6.0 kilograms and this works out to 9.66667 meters per second. So the change in kinetic energy is the final kinetic energy minus the initial kinetic energy and the final kinetic energy is one-half times the total mass because they are stuck together times v prime that we found here squared and subtract from that the total kinetic energy we had to begin with one-half m Av A squared plus one-half m Bv B squared. So we plug in numbers: we have one-half times 2.0 kilograms plus 4.0 times this speed v prime that we found here squared minus one-half times 2.0 kilograms times 15 meters per second squared plus one-half times 4.0 times 7.0 meters per second squared and that is negative 43 joules is the change in kinetic energy. So 43 joules of kinetic energy is lost after the collision.