Question
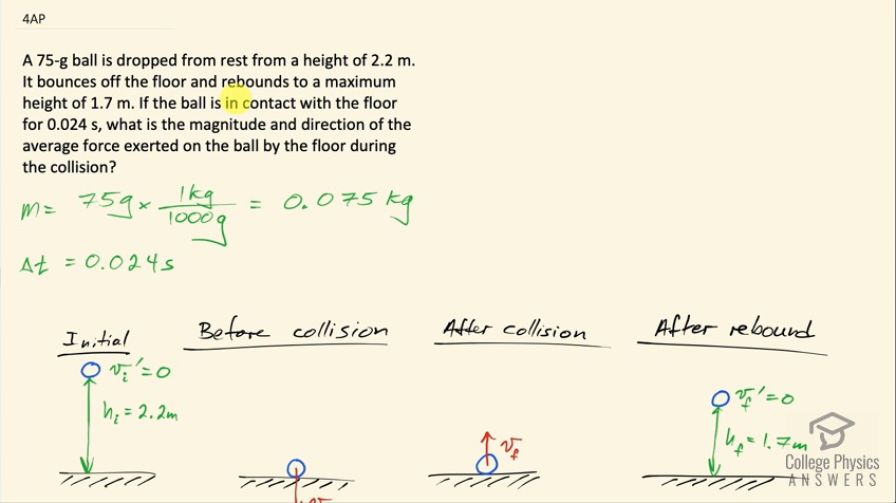
A 75-g ball is dropped from rest from a height of 2.2 m. It bounces off the floor and rebounds to a maximum height of 1.7 m. If the ball is in contact with the floor for 0.024 s, what is the magnitude and direction of the average force exerted on the ball by the floor during the collision?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 4 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 75.0 gram ball is dropped beginning at rest from a height of 2.2 meters and it bounces off the floor and rebounds to a height of 1.7 meters and the ball is in contact with the floor for 0.024 seconds. So what is the force exerted on the ball by the floor during this collision? So to find that force, we need to know what is the change in momentum of the ball but in order to figure that out, we need to know the speed of the ball just before the collision and the speed right after the collision. So first of all, I am writing down the things that we know... just teasing the information out of this question and writing it down to assign to variables that we'll be using in our calculations so m is 75 grams times 1 kilogram for every 1000 grams, which is 0.075 kilograms and the time is 0.024 seconds. So this picture here illustrates what happens initially: the ball is held at rest so v initial and I gave it a prime here because this speed here, I want to call v initial because this is the speed we'll be using in our initial momentum. So normally, if you are thinking only about this picture here, you would say this is v initial and this would be v final but I am choosing to call this v initial for the purpose of the momentum calculation that we will be doing in a minute so that makes this one v initial prime and the ball is going to get dropped from 2.2 meters then it's going to hit this floor at some speed, which we'll call v i. And then after it's been in contact with the floor for 0.024 seconds, it will be launched back upwards at some speed we'll call v f— this is the final speed after the collision— and then it will return to some height that we are told, which is 1.7 meters and it will have a speed of zero at that point. So we need to use these heights to figure out what are v i and v f in order to figure out the initial and final momenta. So when the ball is in contact with the ground, there's a force exerted upwards— a normal force exerted by the ground— and there's also the force of gravity downwards mg and the net force, which is what this change in momentum overtime tells us is the net force. The net force is the up force minus the down force so that's the normal force minus gravity, which is mg. And then another expression for the net force is in terms of the momentum—it is the rate of change in momentum. This is actually the first way in which Newton expressed his second law he said that net force is the rate of change of momentum, he didn't say F net equals mass times acceleration, he said ΔP over Δt. So this is mv final minus mv initial over Δt. So with this being F net and this also being F net, we can equate these two together which we do here and it's the normal force we are interested in and we'll add mg to both sides here and we have the normal force then is m, which you can factor out from both of these terms times v f minus v i over Δt plus g— acceleration due to gravity. Now v f squared equals v initial squared plus 2ad— this is the kinematics formula we are gonna be working with— but we are going to restate these variables in terms of our picture here. So v f—and I hope this isn't too confusing— but v f is gonna be this speed here, which I have labeled v i and the initial speed is v i prime. So this is during the initial drop that we are working with here and then we will add to that 2 times the acceleration, which is negative g times the change in position which is a final position of zero minus an initial position of h i, which is the initial height that it was dropped from. And so this is zero, which I write here and then we have v initial then— after you take the square root of both sides— is the negative square root of 2gh i and this negative comes from the fact that when you take the square root of both sides of an equation, you can choose either the positive or the negative depending on the physical interpretation of the situation and mathematically speaking, it could be one or the other because you know, if you have x squared equals a 4, it's clear that x could either be 2 or it could be negative 2, the square of each of these gives positive 4 so you don't know which one it is but in this case, the Physics shows that the speed is... the velocity is down and so this is going to be negative. Alright... there! Then we have to figure out what is v f in this picture and so we can say zero, which is the final speed at the top of the rebound here— v f prime I have labeled it or 0 in other words— equals v f, which is this speed here after the collision which in the context of just these two pictures is the initial rebound velocity but I am calling it v f because we want to use it in the momentum calculation. So v f squared plus 2 times negative g— acceleration because of gravity— and then times the change in position, which is the final position of the h f minus the initial position of 0. So v f squared equals positive 2gh f after you add 2gh f to both sides and then take the square root of both sides and we are taking the positive square root in this case because we can see that v f is going upwards. Alrighty! So we can substitute this and this into our formula for the normal force exerted by the floor and we replace these two terms here. So the force exerted by the floor then is 0.075 kilograms times the square root of 2 times 9.8 meters per second squared times 2.2 meters plus square root of 2 times 9.8 meters per second squared times 1.7 meters and all that's divided by 0.024 seconds plus 9.8 meters per second squared giving us 39 newtons is the force exerted by the floor.
