Question
A group of students has two carts, A and B, with wheels that turn with negligible friction. The carts can travel along a straight horizontal track. Cart A has known mass mA. The students are asked to use a one-dimensional collision between the carts to determine the mass of cart B. Before the collision, cart A travels to the right and cart B is initially at rest. After the collision, the carts stick together.
- Describe an experimental procedure to determine the velocities of the carts before and after a collision, including all the additional equipment you would need. You may include a labeled diagram of your setup to help in your description. Indicate what measurements you would take and how you would take them. Include enough detail so that another student could carry out your procedure.
- There will be sources of error in the measurements taken in the experiment, both before and after the collision. For your experimental procedure, will the uncertainty in the calculated value of the mass of cart B be affected more by the error in the measurements taken before the collision or by those taken after the collision, or will it be equally affected by both sets of measurements? Justify your answer.
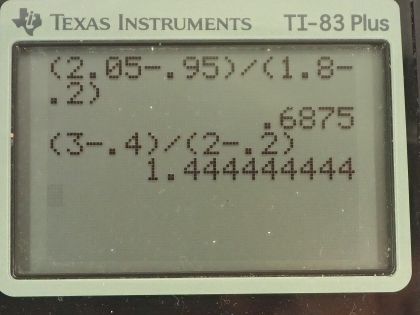
- A group of students took measurements for one collision. A graph of the students’ data is shown below in Figure 8.22. Given , use the graph to calculate the mass of cart B. Explicitly indicate the principles used in your calculations.
- The students are now asked to Consider the kinetic energy changes in an inelastic collision, specifically whether the initial values of one of the physical quantities affect the fraction of mechanical energy dissipated in the collision. How could you modify the experiment to investigate this question? Be sure to explicitly describe the calculations you would make, specifying all equations you would use (but do not actually do any algebra or arithmetic).
Final Answer
- Add an ultrasonic velocity sensor to the list of equipment. Step 1: measure after its initial push. Step 2: measure of the combined carts after collision.
- Uncertainty in will be affected most by the error in measuring . The absolute error in and should be the same, which means the fractional error in will be greater since will be smaller than .
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 18 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A group of students has two carts— labeled A and B— with wheels that turn with negligible friction and they are gonna travel on this horizontal track and cart A has a mass that we know so we know what m A is and we are meant to find out what is the mass of m B assuming that these carts stick together after the collision. So we'll need an ultrasonic velocity sensor that's something that we'll have to add to this experimental setup and the first thing we'll do is measure what is the velocity of cart A so this would be given a push and then it will travel with constant velocity and we'll measure that and then after sticking together, we will use this ultrasonic velocity sensor to also figure out the velocity of this combined mass after collision so we'll measure v prime in other words. And there's going to be sources of error in the measurements— both before and after collision— and we have to figure out what will affect the error in the mass calculation m B the most. So the error in v A—there's only two things that we are measuring v A and v prime although I guess we have also measured m A, there's some error in the mass of cart A as well— and the error from this ultrasonic velocity sensor should be approximately the same absolute amount for both velocity measurements; typically your error estimate should be plus or minus one of the most precise digit in your measuring device if you don't have any other reason to assume that there's more error than that, you could also take the same measurement of the same thing repeated times and then if you find a spread in your measurements then you could use that spread size as your error... we are half the spread size. There's various ways of estimating, I mean it's just an educated anyway. Okay! So we have the same absolute error which is, you know the word absolute is referring to the amount... like the number of meters per second error and now since v prime is going to be smaller because it's the velocity of the two masses combined, the percent error in v prime will be higher because it's gonna be the same absolute error divided by a smaller velocity resulting in a higher percent error in v prime and so it's the error in v prime that's gonna have most impact on the error in our mass B calculation. We could also look at this down here looking ahead a bit this is a formula for calculating what mass B is in terms of mass A and the two velocities and we are dividing by v prime and when you are dividing by a number that has some error, you are going to take the fractional error in that number and add that to the fractional error that you have for m B or for the result. So when dividing things, propagation of error is by adding fractional errors. Okay... and so the fractional error in v prime is going to be higher than the fractional error in v A So part (c) is asking given that we know mass A is 0.5 kilograms, use this graph to calculate the mass of cart B. So we need to know the velocity before collision, which is indicated by these bright red dots and then figure out the velocity after collision indicated by these black dots with a red outline and I have created two lines here— one for each scenario— to get the slope during that time. So the slope when we have only cart A moving is given by this blue line and then the slope for after the two carts are combined after collision is this black line. So v prime is the slope of the black line, it's the change in position over time and so we have to find some values on this graph that are easy to read off and use those in our Δx and our Δt here. This black line is a best fit line, it's meant to have approximately an equal number of dots above and below the line and then it just seems to go through them nicely. Okay! So I've read off this value at 1.8 seconds this looks like it's about 2.05 meters... it's slightly above 2.0 so we'll call it 2.05 and then from that we'll subtract the position at 0.2 seconds and that is approximately 0.95— almost 1 but not quite— and then we divide that by the change in time of 1.8 seconds minus 0.2 seconds this is 0.69 meters per second. Okay! And the slope of blue line, which is the speed of just cart A is 3.0 meters at 2.0 seconds so we have 3.0 meters minus 0.4 meters at 0.2 seconds and then divide that by 2.0 minus 0.2 seconds and we get 1.4444 meters per second. So the momentum before collision equals the total momentum after collision and we are going to use these velocities in our work here. So we have cart A mass times the initial speed of cart A plus m Bv B equals m Av prime plus m Bv prime because cart A and B are both traveling at the same speed and we want to solve for m B though so we gotta subtract m Av prime from both sides and then also substitute in zero for m Bv B because cart B is initially at rest then we can factor out m A from both terms here and we have m B equals m A times v A minus v prime and then we are also dividing both sides by v prime so we have m A times v A minus v prime all over v prime. So that's 0.50 kilograms times 1.4444 meters per second minus 0.69 meters per second divided by 0.69 and that is 0.55 kilograms. Part (d) asks us to consider how much kinetic energy is lost, what is the fractional change in kinetic energy? And we'll take... the initial kinetic energy minus the final kinetic energy one-half times this total mass times the speed after collision squared and divide that by the kinetic energy we started with and we can make a substitution for v prime in terms of the masses in v A because this is our conservation of momentum expression here— the initial total momentum was just that of cart A— and the total final momentum is the mass of the two carts stuck together times their common velocity that they move together with after collision—v prime— and we can divide both sides by m A plus m B. So v prime then is m Av A over m A plus m B and we can replace v prime with this expression now and we do that here. And we have m A plus m B is squared in the denominator and it's to the power of 1 here and so we are left with m A plus m B to the power of 1 in the end here and on top, we have m A squared times v A squared and this denominator can be divided into both terms on the top and the left term is the same so it becomes 1 and then minus m A over m A plus m B because this m A will cancel with one of these m A's to make it exponent 1 we have a v A squared canceling with this v A squared and this one-half canceling with this one-half and we are left with m A to the power of 1 over m A plus m B. And if you wanted to write this as a single fraction, multiply this by m A plus m B all over m A plus m B and then we have m A plus m B minus m A all over m A plus m B and these m A's make zero, we are left with m B over m A plus m B. Alright! So this is the fractional change in kinetic energy for a perfectly inelastic collision. And we could verify this by placing a whole bunch of weights on cart A and verify that for each one of them, we reduce the fractional change in kinetic energy as the mass A increases.