Question
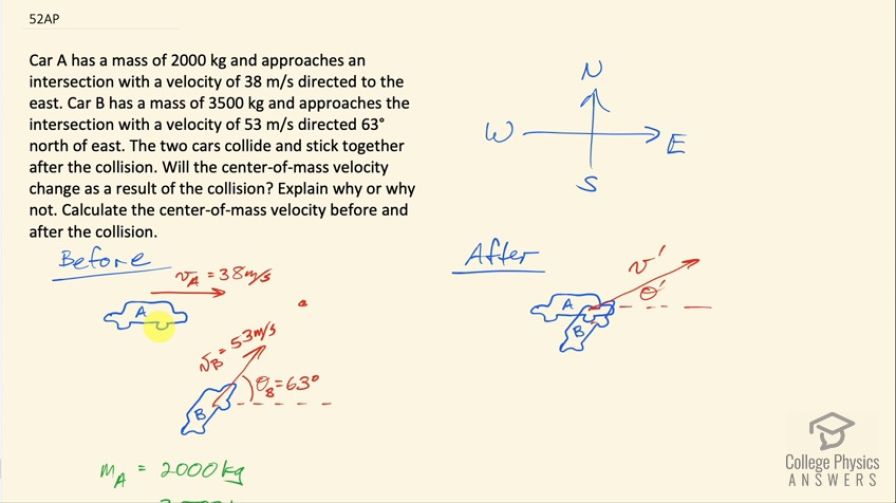
Car A has a mass of 2000 kg and approaches an intersection with a velocity of 38 m/s directed to the east. Car B has a mass of 3500 kg and approaches the intersection with a velocity of 53 m/s directed 63° north of east. The two cars collide and stick together after the collision. Will the center-of-mass velocity change as a result of the collision? Explain why or why not. Calculate the center-of-mass velocity before and after the collision.
Final Answer
The center of mass velocity doesn't change after the collision since, given that , momentum is conserved and mass remains constant.
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 52 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
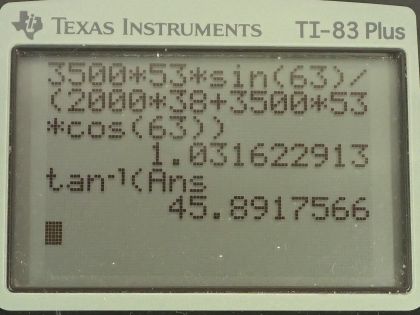
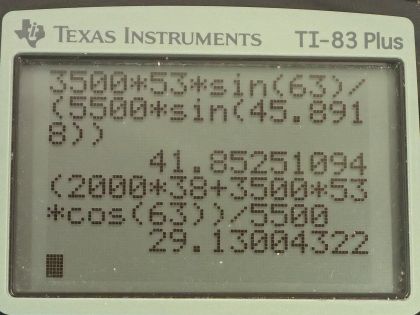
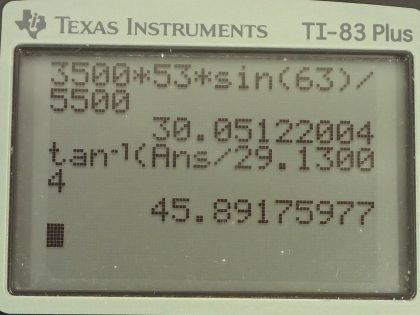
This is College Physics Answers with Shaun Dychko. A 2000 kilogram car is approaching an intersection here at a speed of 38 meters per second and it's moving horizontally— it's moving straight to the East— and car B that has a mass of 3500 kilograms is moving at a velocity 63 degrees towards the North compared to East and so it's moving in this direction towards this intersection here at a speed of 53 meters per second; the cars will collide and then stick together and then move off with some velocity v prime at an angle Θ prime above the horizontal and this arrow is just drawn a little bit... this angle is a little bit smaller than the initial angle because there is going to be a greater x-component to the momentum after collision contributed by this car A versus the x-component that existed originally in this vector here. Alright! So our job is to figure out what the center of mass velocity is before and after the collision and ask whether or not the center of mass velocity will change as a result of the collision. So I am gonna start with figuring out what v prime and Θ prime are and this is the center of mass velocity after collision since there's only one object to consider: it's this mass that consists of the car A and B combined together. So we know that the x-component of the initial total momentum will equal the x-component of the final total momentum and likewise for the y-direction, we have the initial y-component of momentum in total equals the total y-component of momentum after collision. So considering the x-direction, we have car A's mass times its velocity plus car B's mass times its velocity times cosine of Θ B because we want to find the x-component of this v B so it's this component here that we are interested in and this is the adjacent leg of this right triangle in yellow here and we use cos of this angle multiplied by the hypotenuse to figure out the length of this adjacent leg that goes to here. So this is v x... v B x I should say x-component of velocity B. Okay! Good! So that got substituted there and then in the y-direction, we have no component of... car A's momentum is in the y-direction because it's moving entirely horizontally whereas car B has its mass times its velocity multiplied by sin of Θ B to get length of this opposite leg for the y-component of its velocity. That's going to equal the total mass when the two cars are combined times v prime times sin Θ prime and up here by the way, we had the total mass times v prime times cos Θ prime we have this being the x-component of the final velocity and this being the y-component of the final velocity and we are using cos to get the x-component and sin to get the y-component each of which are multiplied by the hypotenuse and... there we go! So we are gonna solve for Θ prime first: we are gonna do that by dividing equation two by equation one. So... the left side of equation two is m Bv B sin Θ B and we are dividing it by the left side of equation one m Av A plus m Bv Bcos Θ B and on the right hand side, we have the right side of equation two total mass times v prime times sin Θ prime divided by total mass times v prime times cos Θ prime and sin divided by cos can be replaced with tangent Θ prime— that's a trigonometric identity— and so I have replaced sin Θ prime over cos Θ prime with tan Θ prime and switched the sides around and it equals m Bv B sin Θ B over all this stuff. Then plug in some numbers: we have 3500 kilograms is the mass of car B times its speed of 53 meters per second times sin 63 degrees divided by 2000 kilograms times 38 meters per second— this is the mass and speed of car A— plus 3500 kilograms times 53 meters per second times cos 63 degrees and that gives this number and we take the inverse tangent of that to figure out what Θ prime is it's 45.8918 degrees. And now we need to know the speed after collision and that's v prime and we'll use equation two, rearrange for v prime to figure that out. So we'll divide both sides by m A plus m B times sin Θ prime and then we have this equation here. So that's 3500 kilograms times 53 meters per second times sin 63 divided by the total mass times sin of this angle that we found here after the collision that works out to 41.8525 meters per second. So this v prime is the center of mass velocity after collision and it is 41.9 meters per second, 45.9 degrees North of East. So the next question is what is the center of mass velocity before the collision? Well, the total mass times the x-component of the center of mass velocity before collision— and we know this is before collision because I don't have a prime symbol written there— this equals the x-component of car A's momentum and the x-component of car B's momentum; car A is moving entirely in the x-direction so it's m Av A and car B is m Bv B x-component and v B x-component is v B times cos Θ B for the same reasons that we talked about earlier. Okay! And then dividing both sides by this total mass but I substituted in m A plus m B in place of m total here. So that's 2000 kilograms times 38 meters per second plus 3500 kilograms times 53 meters per second times cos 63 divided by the total mass and that's 29.13004 meters per second is the x-component of the center of mass velocity before collision. Now in the y-direction, we have zero momentum for car A plus m Bv B sin Θ B— this is the y-component of car B's momentum before the collision— and we divide both sides by the total mass and then substituting m A plus m B in place of m total and we get car B's mass times its speed times sin 63 divided by the total mass and that is 30.0512 meters per second is the y-component of the center of mass velocity before collision. So the direction or Θ for this center of mass velocity before collision is the inverse tangent of the y-component divided by the x-component. So that's inverse tangent of 30.0512 meters per second divided by 29.13004 meters per second and that's 45.8918 degrees. And the magnitude of the center of mass velocity before collision is the square root of the x- and y-components each squared and added together. So that's the square root of the x-component 29.13004 squared plus the y-component squared and that's 41.8525 meters per second. So the center of mass velocity before collision is 41.9 meters per second, after you round it to the tenths place in a direction of 45.9 degrees North of East and this is the same as the center of mass velocity after the collision and so we can see that since momentum is conserved and the mass hasn't changed— it means the mass could change if some weight was just dropped from above onto a car after the collision or something— and so since momentum is conserved and the mass hasn't changed then the center of mass velocity also has to stay the same after the collision.