Question
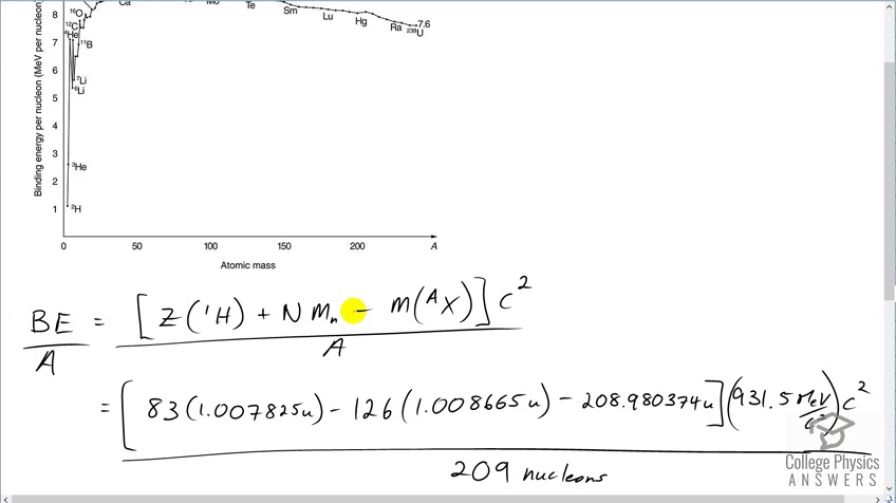
is the heaviest stable nuclide, and its BE / A is low compared with medium-mass nuclides. Calculate BE/A ,
the binding energy per nucleon, for and compare it with the approximate value obtained from the graph in Figure 31.26.
Final Answer
This matches the value on the graph.
Solution video
OpenStax College Physics, Chapter 31, Problem 71 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the binding energy per nucleon of bismuth-209. This numerator is the binding energy which is the number of protons in bismuth multiplied by the atomic mass of hydrogen plus the number of neutrons in the bismuth nuclide times the mass of a bare neutron minus the mass of whatever bismuth is— the atomic mass of bismuth. Then we multiply that by c squared to turn it into energy and divide by the number of nucleons. So we have 83 times 1.007825 atomic mass units; this is the atomic mass of hydrogen including the electron that is around the hydrogen nucleus and we subtract away those 83 electrons though which are also included in this number because bismuth also has 83 electrons included in this mass. And so we have 83 electrons that we don't really want them as I have included here and then we take them away over here. So they cancel out anyway. OK. And then minus a 126 neutrons multiplied by the mass and atomic mass units for each neutron minus the atomic mass of bismuth, convert it into megaelectron volts per c squared for every atomic mass unit times by c squared divided by 209 nucleons giving us 7.848 megaelectron volts per nucleon and this matches the value on the graph roughly; bismuth is around here so just after mercury and extrapolating this back to the axis, it's about 7.8 or so.
