Question
The particles emitted in the decay of (tritium) interact with matter to create light in a glow-in-the-dark exit
sign. At the time of manufacture, such a sign contains 15.0 Ci
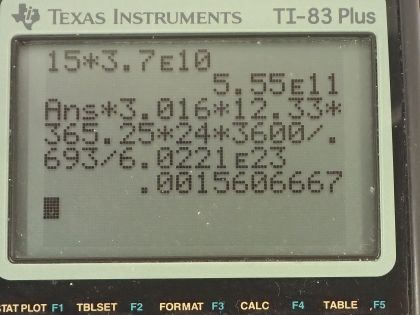
of . (a) What is the mass of the tritium? (b) What is its
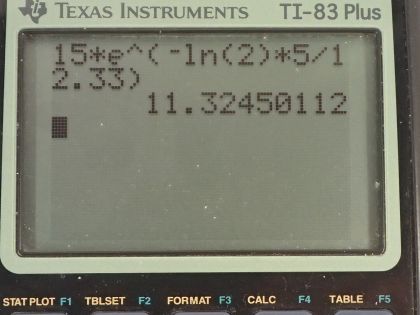
activity 5.00 y after manufacture?
Final Answer
Solution video
OpenStax College Physics, Chapter 31, Problem 58 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Some tritium with an activity of 15.0 curies is being used to make an exit sign glow in the dark; the half-life of tritium is 12.33 years and it has a molar mass of 3.016 grams per mol. I converted the activity into becquerels by multiplying by 3.70 times 10 to the 10 becquerels per curie and we have to figure out what is the mass of tritium being used given that it has this much activity? So the activity of a substance is 0.693 multiplied by the number of atoms divided by the half-life and the number of atoms is the mass and this is what we are going to solve for divided by the molar mass times Avogadro's number so we can substitute this in place of N here and then multiply top and bottom by the molar mass and you end up with this equation here. Now we are going to rearrange this to solve for m—the mass— by multiplying both sides by the half-life times the molar mass of tritium divided by 0.693 times Avogadro's number so both sides get multiplied by that— this and this— and then switch the sides around and we end up with the mass then is the activity times the molar mass times the half-life divided by 0.693 times Avogadro's number. So that's 5.55 times 10 to the 11 becquerels times 3.016 grams per mol times the half-life converted into seconds divided by 0.693 times Avogadro's number and we have 1.56 milligrams— this is how much tritium is in the exit sign. And then part (b) asks in 5 years, what will the activity of the sample be? Well activity in the future is the activity now times e to the negative of this decay factor multiplied by time, this decay factor λ is natural logarithm of 2 divided by half-life so we substitute that in place of λ and the activity then is 15.0 curies— activity that it has today— times e to the negative natural logarithm of 2 over 12.33 years—half-life— times the amount of time that's going to pass, which is 5.00 years and this is 11.3 curies will be the activity in 5 years.