Question
Suppose a particle of ionizing radiation deposits 1.0 MeV in the gas of a Geiger tube, all of which goes to creating ion pairs. Each ion pair requires 30.0 eV of energy. (a) The applied voltage sweeps the ions out of the gas in . What is the current? (b) This current is smaller than the actual current since the applied voltage in the Geiger tube accelerates the separated ions, which then create other ion pairs in subsequent collisions. What is the current if this last effect multiplies the number of ion pairs by 900?
Final Answer
Solution video
OpenStax College Physics, Chapter 31, Problem 4 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
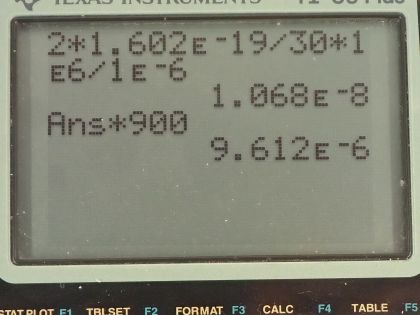
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A particle of ionizing radiation deposits 1.0 megaelectron volt of energy into the gas in the Geiger tube and it creates ion pairs; each ion pair requires 30.0 electron volts to create it per pair. So question in part (a) is what current will there be knowing that there is potential difference applied across the gas which will then move the charges in opposite directions so the ion pairs will have a positive and a negative part to each pair and the positive charges will go one way towards the negative plate and so these are all connected to a potential difference here—this battery— and this is the negative plate here and it will attract the positive charges towards it and then the negative ion will go the other way to the positively charged plate. So there will be two currents here: one with positive ions flowing one way and negative ions flowing the other way and you get two currents from each pair that is created and so we are not really told what the charge is on each ion but let's assume that each charge is 1 times the elementary charge so this is charge of one electron and this is the charge of one proton so positive q e and this is negative q e. Okay! So because we have two currents for— one for each of the signs of the charge— we multiply the elementary charge by 2 to get the number of coulombs for each pair of ions created so that's 2 times 1.602 times 10 to the minus 19 coulombs per pair. Then we multiply that by 1 pair for every 30.0 electron volts and the pairs cancel then multiply by 1.00 times 10 to the 6— total energy in electron volts that is deposited— and the electron volts cancel and this is the number of coulombs then that are created that will be moving on this numerator and the current is coulombs per time and so we divide by the amount of time it takes for this potential difference to clear all these ions out of the gas and we are told that that time is 1.00 microsecond so that's 1.00 times 10 to the minus 6 seconds so the current is 1.07 times 10 to the minus 8 amps. Now it turns out that the accelerating potential difference here is going to cause these ions to bump into other particles of gas and thereby ionize those particles too to the point where each ion pair produces 900 other ion pairs as a result of these collissions. So to get the current then that will actually occur, I prime will multiply the current that we would expect only from the ion pairs by 900. So 900 times the answer to part (a) gives 9.6 microamps.