OpenStax College Physics, Chapter 31, Problem 40 (Problems & Exercises)

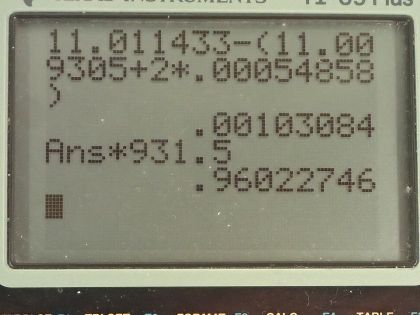
This is College Physics Answers with Shaun Dychko. We need to write the equation for positron decay of carbon-11. We can look up in appendix A how many protons there are in carbon-11; its atomic number is 6 so that means it has 6 protons and that leaves 5 neutrons left over when you take 6 away from the total number of nucleons which is 11. And so with a positron decay, a positron is made which is the anti-electron— anti-matter counterpart to an electron— and this positive charge arises from a proton turning into a neutron and since charge has to be conserved, it's this proton that turns into a neutron that goes here. So in order for charge to be conserved, a positron has to be created so there's a total of 6 plus charge in this carbon-11 nuclide and so there needs to be a total of 6 plus charge among all of the daughter products of this reaction— I was going to call this a daughter nuclide but it's not a nuclide, it's a lepton. Okay! So we need to have 1 less proton in this dotted nuclide here and the element with 5 protons is boron and the number of nucleons will stay the same so its mass number doesn't change, it's still 11 but there are now 6 neutrons. So we explain that the positron is created to conserve charge now this electron-neutrino is created in order to conserve electron family number. On the left side, there are no electrons so there's no electron family number and on the right hand side, this positron has an electron family number of negative 1 and so there's an electron-neutrino created to compensate for that negative 1 by having a positive 1 here for a total of 0 in terms of electron family number. So electron family number is conserved: it's a total of 0 on the left and it's a total of 0 on the right. Okay! Part (b) asks how much energy is released in this reaction? There's little bit of confusing business around this mass of an electron that's added here 2 times we have to find the difference in mass between these nuclides and then add on the mass of this positron which has the same mass as an electron. But we don't know what the mass of the nuclides are instead what we are given in this data table here is the mass of the atoms which are the nuclides with the surrounding electrons as well so for the carbon-11, this mass includes 6 electrons and for the boron-11, well it includes only 5 electrons now. So when we take the mass of carbon-11 it includes 6 electrons that we want to get rid of we are going to get rid of those masses because we want to just have the mass of the nuclide and often it's just a wash when you are doing this difference in mass because often the daughter nuclide will have the same number of electrons as the parent nuclide in which case the electron masses just subtract to 0 leaving behind only the difference in mass of the nuclides but in this case boron has only 5 electrons so we need to add 1 electron to the atomic mass of boron in order to compensate fully for all 6 electrons in the carbon-11 and then furthermore, we have to add an electron mass due to the positron created in this reaction. So that is why there are 2 electron masses here: one to compensate for the fact that boron has only 5 electron masses in its atomic mass whereas we need to have 6 in order to subtract away the 6 electrons included in the carbon atomic mass and then additionally, we need 1 more electron mass to account for the mass of this positron. Alrighty! So we look up in that data table the mass of carbon-11 and then minus the atomic mass of boron-11 plus 2 times the atomic mass of an electron— not sure if you should call it an atomic mass but anyway, it's in atomic mass units anyhow— and we have 0.0010308 atomic mass units is the difference in mass between the parent and all of the products. Let's multiply that by 931.5 megaelectron volts per c squared for every atomic mass unit then multiply that by c squared in our formula and then we end up with 0.960 megaelectron volts of energy released.