OpenStax College Physics, Chapter 31, Problem 50 (Problems & Exercises)

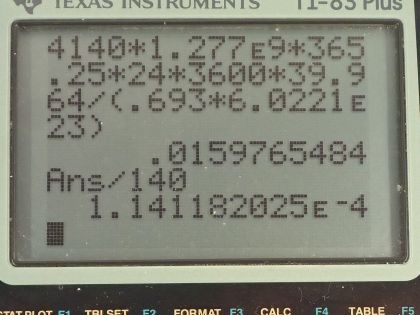
This is College Physics Answers with Shaun Dychko. The radioactive isotope of potassium in a person's body has an activity of 4140 becquerels suppose and the question is what mass of potassium-40 is in a person given a half-life of potassium-40 of 1.277 times 10 to the 9 years and the molar mass of potassium-40 is 39.964 grams per mol, which I looked up in the appendix at the end of the textbook. So we are going to use this formula which says the activity of something that's radioactive is 0.693 multiplied by the number of atoms divided by a half-life and we'll express the number of atoms in terms of mass and then eventually solve for the mass. So if we take the mass and divide it by the molar mass that will give us the number of moles of the substance and then multiply by Avogadro's number which is the number of atoms per mol and this will give us atoms. So you can substitute all this in place of N here and then we need to solve for m—the mass. So let's multiply both sides by the molar mass which cancels with this here and multiply the other side by molar mass as well and multiply by half-life as well and then divide both sides by 0.693 and also divide by Avogadro's number and then we end up with this line here after we switch the sides around and the mass of potassium-40 is its activity multiplied by its half-life times the molar mass divided by 0.693 times Avogadro's number. So that's 4140 becquerels times 1.277 times 10 to the 9 years and we have to convert the years into seconds in order to have units that will work with the becquerels because becquerels is an mks unit— meters, kilograms and seconds— it's the number of decays per second so we need to multiply that by seconds. So we multiply the half-life in years by 365.25 days per year times 24 hours per day times 3600 seconds per hour and then we multiply by the molar mass of 39.964 grams per mol divide 0.693 times Avogadro's number—6.0221 times 10 to the 23 atoms per mol— and we are left with the mass in grams so that is 16.0 milligrams. Then we are asked in part (b) to figure out what fraction is this radioactive isotope of the total amount of potassium? So we are told there's about 140 grams of potassium in a typical 70.0 kilogram adult so we take 0.015977 grams divide it by 140 grams and that's 1.14 times 10 to the minus 4.