Question
(a) Calculate BE / A for , the rarer of the two most common uranium isotopes. (b) Calculate BE / A for . (Most of uranium is .) Note that has even numbers of both protons and neutrons. Is the BE / A of significantly different from that of ?
Final Answer
- The binding energy for is 0.28% greater than that of . This is not significant since greater stability would be expected with a greater binding energy per nucleon, but the half life of is shorter than .
Solution video
OpenStax College Physics, Chapter 31, Problem 72 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
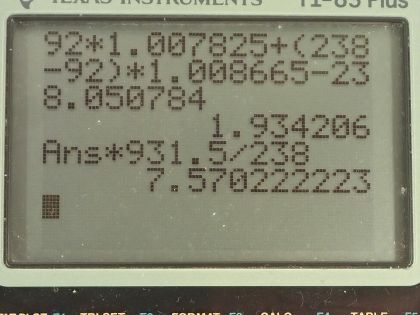
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the binding energy per nucleon for uranium-235. We need to know what its atomic mass is so I looked that up in the appendix at the end of the textbook here and uranium-235 has an atomic mass of 235.043924 atomic mass units; it also has an atomic number of 92 so that means it has 92 protons. So the binding energy per nucleon is this mass defect where this difference in mass between the nucleons in their free state unbound to anything and then subtract from that the atomic mass of the package of all the nucleons bound together in this atom of uranium-235. So I am using the word 'atom' sort of interchangeably with nucleons and it's important to understand that these masses that are in this appendix here are the atomic masses which means they include the mass of electrons and that's... the electrons are a nuisance here because we don't want to deal with the mass of the electrons but things are okay because we will use the atomic mass of hydrogen here which is the mass of 92 protons plus the mass of 92 electrons included in that and then we have a total of 92 electron masses included in this atomic mass for uranium as well and so we add the electrons here and then we subtract them away over here so they come out in the wash... or it's a wash I should say and the electron masses subtract away. So we have 92 hydrogen atom masses here plus the number of neutrons, which is the mass number 235 minus the atomic number 92 multiplied by the mass of a neutron— 1.008665 atomic mass units— and then from that we subtract the mass of uranium-235 atom and that difference in mass then is 1.915071 atomic mass units. So we take that mass, multiply it by 931.5 megaelectron volts per c squared for every atomic mass unit and then multiply by c squared and we have megaelectron volts in the top divided by the total number of nucleons, which is 235 and we get 7.591 megaelectron volts per nucleon. Then we do the same sort of calculation for uranium-238 which has the same atomic mass unit or same atomic number because it's the same element but a different number of neutrons, it's now 238 minus 92 neutrons. The atomic mass for uranium-238 is 238.050784 atomic mass units and this mass difference then becomes 1.934206 atomic mass units we multiply by 931.5 divided by 238 and it works out to 7.570 megaelectron volts per nucleon. The question also asks is the difference between the binding energy per nucleon between these two isotopes significant? So we have 7.570 on the one hand and 7.591 on the other; let's find the percent difference between them. We take the difference between the two and then divide by this one here for uranium-238 and multiply by 100 percent and that's 0.28 percent difference. And that percent difference is small so the difference is not significant and in fact, you would expect with a higher binding energy per nucleon that uranium-235 would be more stable and it would have a longer half-life if you were to look only at the binding energy per nucleon but the opposite is true it turns out that uranium-238 is in fact more stable and this is on account of it having an even number of protons and neutrons, which for whatever reason makes a nuclide more stable. So in percentage terms, the difference is small and the effect of that difference is not apparent in this half-life so having a higher binding energy per nucleon for uranium-235 should make the half-life longer but it doesn't which means that higher binding energy per nucleon is not significant.