The energy of 30.0 eV is required to ionize a molecule of the gas inside a Geiger tube, thereby producing an ion pair. Suppose a particle of ionizing radiation deposits 0.500 MeV of energy in this Geiger tube. What maximum number of ion pairs can it create?

A particle of ionizing radiation creates 4000 ion pairs in the gas inside a Geiger tube as it passes through. What minimum energy was deposited, if 30.0 eV is required to create each ion pair?

(a) A particle of ionizing radiation creates 4000 ion pairs in the gas inside a Geiger tube as it passes through. What minimum energy was deposited, if 30.0 eV is required to create each ion pair? Convert the energy to joules or calories. (b) If all of this energy is converted to thermal energy in the gas, what is its temperature increase, assuming $50.0 \textrm{ cm}^3$ of ideal gas at 0.250-atm pressure? (The small answer is consistent with the fact that the energy is large on a quantum mechanical scale but small on a macroscopic scale.)

Suppose a particle of ionizing radiation deposits 1.0 MeV in the gas of a Geiger tube, all of which goes to creating ion pairs. Each ion pair requires 30.0 eV of energy. (a) The applied voltage sweeps the ions out of the gas in $1.00\textrm{ }\mu\textrm{s}$. What is the current? (b) This current is smaller than the actual current since the applied voltage in the Geiger tube accelerates the separated ions, which then create other ion pairs in subsequent collisions. What is the current if this last effect multiplies the number of ion pairs by 900?

Verify that a $2.3\times 10^{17} \textrm{ kg}$ mass of water at normal density would make a cube 60 km on a side, as claimed in Example 31.1. (This mass at nuclear density would make a cube 1.0 m on a side.)

Find the length of a side of a cube having a mass of 1.0 kg and the density of nuclear matter, taking this to be $2.3\times 10^{17}\textrm{ kg/m}^3$.

What is the radius of an alpha particle?

Find the radius of a $^{238}\textrm{Pu}$ nucleus. $^{238}\textrm{Pu}$ is a manufactured nuclide that is used as a power source on some space probes.

(a) Calculate the radius of $^{58}\textrm{Ni}$, one of the most tightly bound stable nuclei. (b) What is the ratio of the radius of $^{58}\textrm{Ni}$ to that of $^{258}\textrm{Ha}$, one of the largest nuclei ever made? Note that the radius of the largest nucleus is still much smaller than the size of an atom.

The unified atomic mass unit is defined to be $1 \textrm{ u} = 1.6605\times 10^{-27}\textrm{ kg}$. Verify that this amount of mass converted to energy yields 931.5 MeV. Note that you must use four-digit or better values for $c$ and $\lvert q_e \rvert$.

What is the ratio of the velocity of a $\beta$ particle to that of an $\alpha$ particle, if they have the same nonrelativistic kinetic energy?

If a 1.50-cm-thick piece of lead can absorb 90.0% of the $\gamma$ rays from a radioactive source, how many centimeters of lead are needed to absorb all but 0.100% of the $\gamma$ rays?

The detail observable using a probe is limited by its wavelength. Calculate the energy of a $\gamma$-ray photon that has a wavelength of $1\times 10^{-16}\textrm{ m}$, small enough to detect details about one-tenth the size of a nucleon. Note that a photon having this energy is difficult to produce and interacts poorly with the nucleus, limiting the practicability of this probe.

(a) Show that if you assume the average nucleus is spherical with a radius $r = r_0 A^{1/3}$ , and with a mass of $A\textrm{ u}$, then its density is independent of $A$. (b) Calculate that density in $\textrm{u/fm}^3$ and $\textrm{kg/m}^3$ , and compare your results with those found in Example 31.1 for $^{56}\textrm{Fe}$.

What is the ratio of the velocity of a 5.00-MeV $\beta$ ray to that of an $\alpha$ particle with the same kinetic energy? This should confirm that $\beta$s travel much faster than α s even when relativity is taken into consideration.

(a) What is the kinetic energy in MeV of a $\beta$ ray that is traveling at $0.998c$ ? This gives some idea of how energetic a $\beta$ ray must be to travel at nearly the same speed as a $\gamma$ ray. (b) What is the velocity of the $\gamma$ ray relative to the $\beta$ ray?

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
$\beta^-$ decay of $^3\textrm{H}$ (tritium), a manufactured isotope of hydrogen used in some digital watch displays, and manufactured primarily for use in hydrogen bombs.

Write the complete decay equation for the given nuclide in the complete $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation: $\beta^-$ decay of $^{40}\textrm{K}$, a naturally occurring rare isotope of potassium responsible for some of our exposure to background radiation.

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
$\beta^+$ decay of $^{50}\textrm{Mn}$

Write the complete decay equation for $\beta^+$ decay of $^{52}\textrm{Fe}$ in the complete $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation:

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
Electron capture by $^7\textrm{Be}$

Write the complete decay equation for electron capture by $^{106}\textrm{In}$ in the complete $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation.

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
$\alpha$ decay of $^{210}\textrm{Po}$, the isotope of polonium in the decay series of $^{238}\textrm{U}$ that was discovered by the Curies. A favorite isotope in physics labs, since it has a short half-life and decays to a stable nuclide.

Write the complete decay equation for the given nuclide in the complete $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation: $alpha$ decay of $^{226}\textrm{Ra}$, another isotope in the decay series of $^{238}\textrm{U}$, first recognized as a new element by the Curies, poses special problems because its daughter is a radioactive noble gas.

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
$\beta^-$ decay producing $^{137}\textrm{Ba}$ . The parent nuclide is a major waste product of reactors and has chemistry similar to potassium and sodium, resulting in its concentration in your cells if ingested.

Identify the parent nuclide and write the complete decay equation in the $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation: $\beta^-$ decay producing $^{90}\textrm{Y}$. The parent nuclide is a major waste product of reactors and has chemistry similar to calcium, so that it is concentrated in bones if ingested ($^{90}\textrm{Y}$ is also radioactive.)

Write the complete decay equation for the given nuclide in the complete $^A_Z\textrm{X}_N$ notation. Refer to the periodic table for values of Z:
$\alpha$ decay producing $^{228}\textrm{Ra}$. The parent nuclide is nearly 100% of the natural element and is found in gas lantern mantles and in metal alloys used in jets ($^{228}\textrm{Ra}$ is also radioactive).

Identify the parent nuclide and write the complete decay equation in the $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N}$ notation: $\alpha$ decay producing $^{208}\textrm{Pb}$. The parent nuclide is in the decay series produced by $^{232}\textrm{Th}$, the only naturally occurring isotope of thorium.

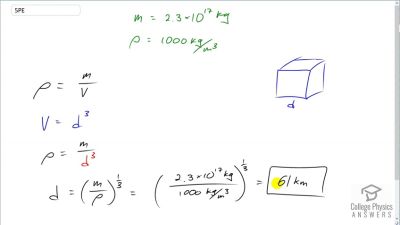
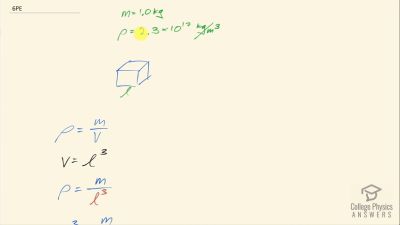
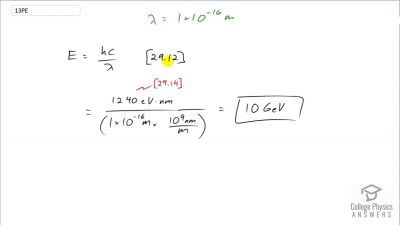
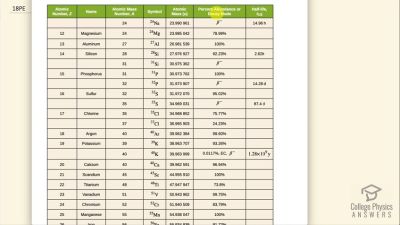
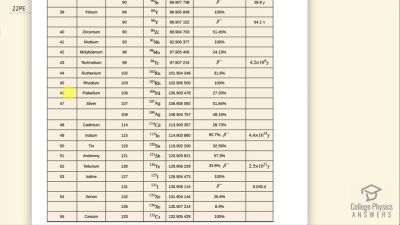
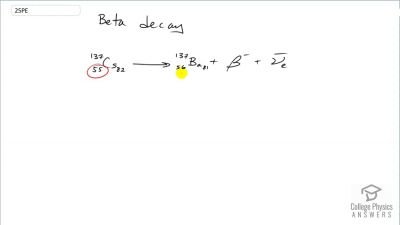
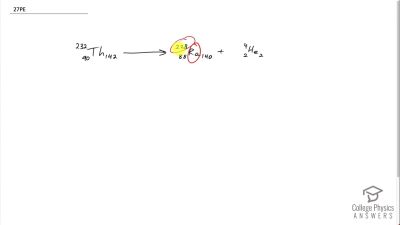
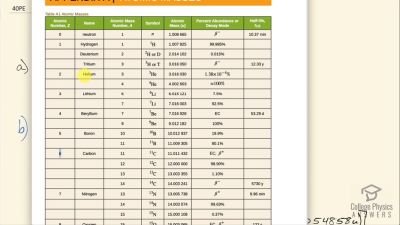
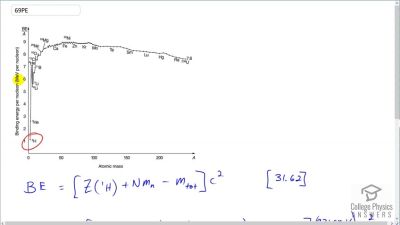
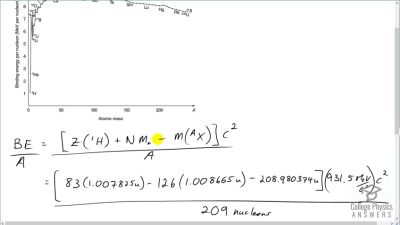
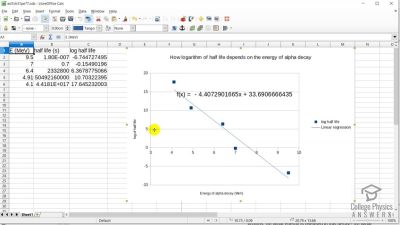
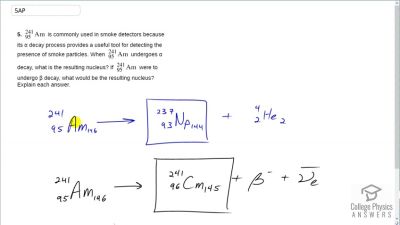
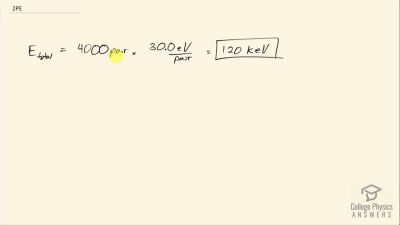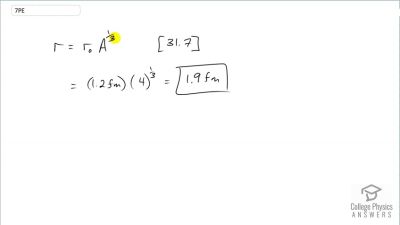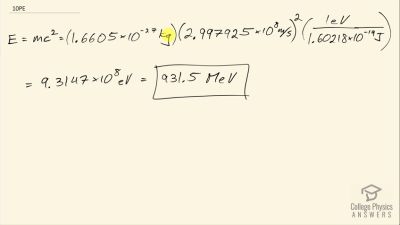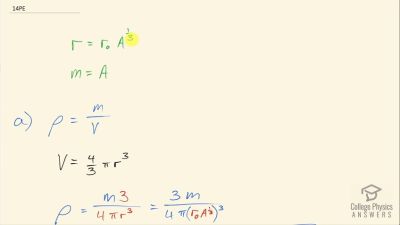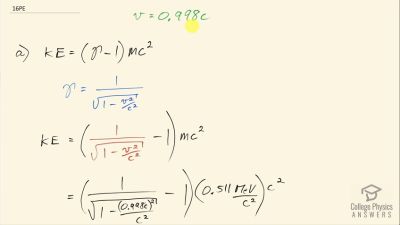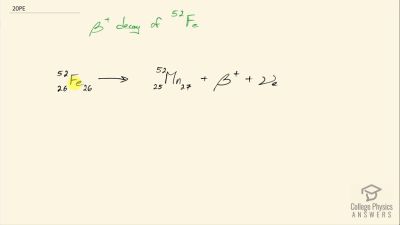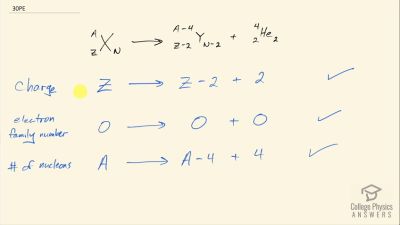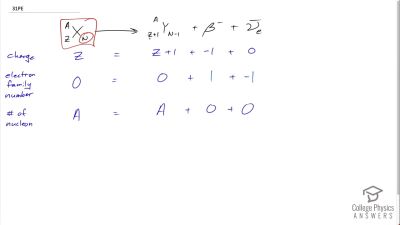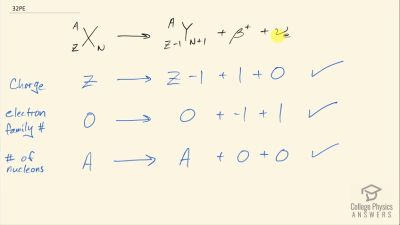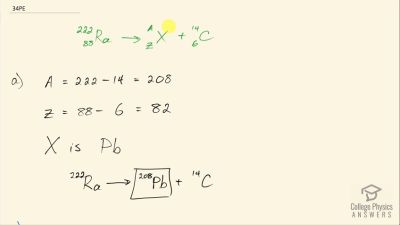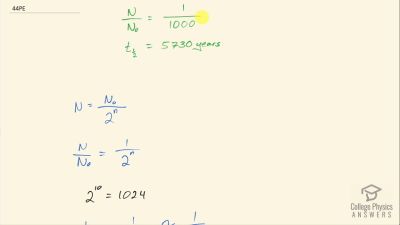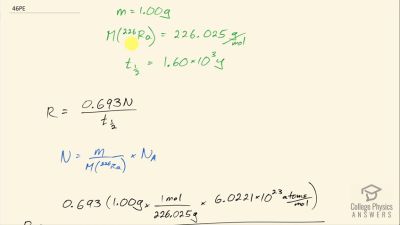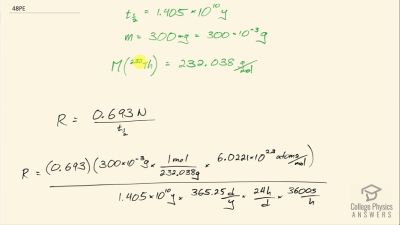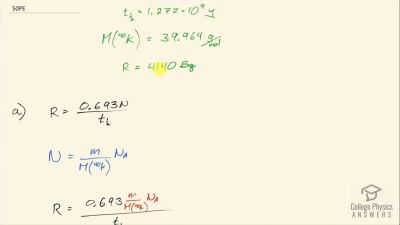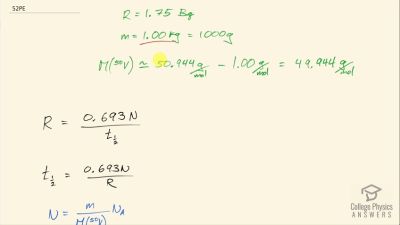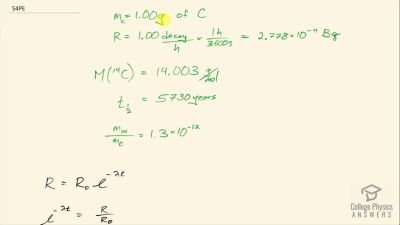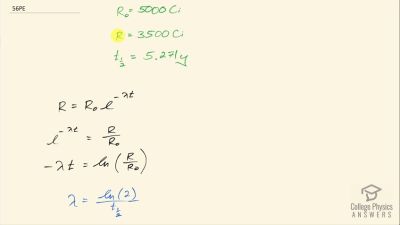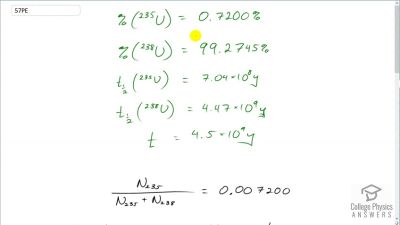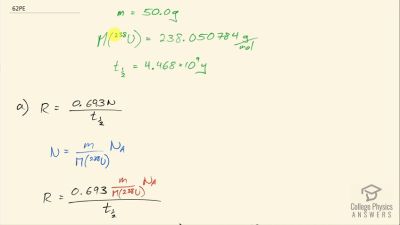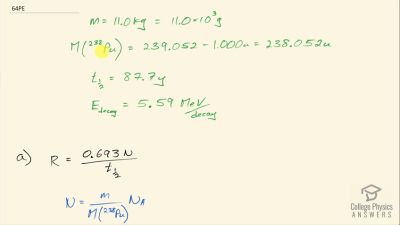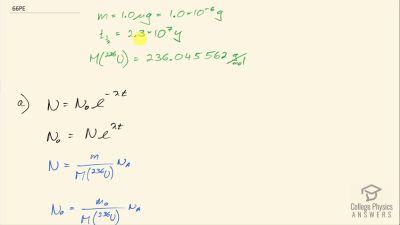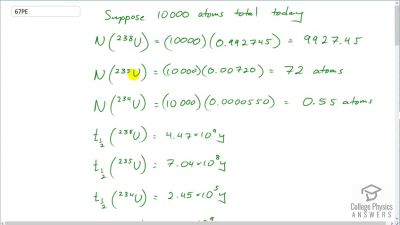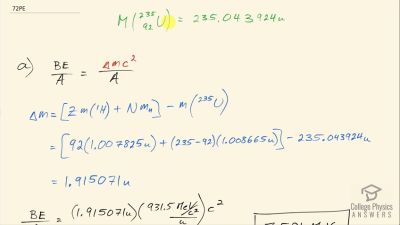When an electron and positron annihilate, both their masses are destroyed, creating two equal energy photons to preserve momentum. (a) Confirm that the annihilation equation $\textrm{e}^+ + \textrm{e}^- \to \gamma + \gamma$ conserves charge, electron family number, and total number of nucleons. To do this, identify the values of each before and after the annihilation. (b) Find the energy of each $\gamma$ ray, assuming the electron and positron are initially nearly at rest. (c) Explain why the two $\gamma$ rays travel in exactly opposite directions if the center of mass of the electron-positron system is initially at rest.

Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for α decay given in the equation $^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N} \to {}^{\textrm{A}-4}_{\textrm{Z}-2}\textrm{Y}_{\textrm{N}-2} + {}^4_2\textrm{He}_2$. To do this, identify the values of each before and after the decay.

Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for $\beta^-$ decay given in the equation ${}^A_Z\textrm{X}_N \to {}^A_{Z+1}\textrm{Y}_{N-1} + \beta^- + \bar{\nu_\textrm{e}}$. To do this, identify the values of each before and after the decay.

Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for β− decay given in the equation ${}^\textrm{A}_\textrm{Z}\textrm{X}_\textrm{N} \to {}^\textrm{A}_{\textrm{Z}-1}\textrm{Y}_{\textrm{N}+1} + \beta^+ + \nu_e$. To do this, identify the values of each before and after the decay.

Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for electron capture given in the equation $^A_Z\textrm{X}_N + e^- \to ^A_{Z-1}\textrm{Y}_{N+1} + \nu_e$. To do this, identify the values of each before and after the capture.

A rare decay mode has been observed in which $^{222}\textrm{Ra}$ emits a $^{14}\textrm{C}$ nucleus. (a) The decay equation is ${}^{222}\textrm{Ra} \to {}^{\textrm{A}}\textrm{X} + {}^{14}\textrm{C}$. Identify the nuclide ${}^\textrm{A}\textrm{X}$. (b) Find the energy emitted in the decay. The mass of ${}^{222}\textrm{Ra}$ is $222.015353\textrm{ u}$.

(a) Write the complete $\alpha$ decay equation for $^{226}\textrm{Ra}$ . (b) Find the energy released in the decay.

(a) Write the complete $\alpha$ decay equation for ${}^{249}\textrm{Cf}$. (b) Find the energy released in the decay.

(a) Write the complete $\beta^-$ decay equation for the neutron. (b) Find the energy released in the decay.

(a) Write the complete $\beta^-$ decay equation for ${}^{90}\textrm{Sr}$, a major waste product of nuclear reactors. (b) Find the energy released in the decay.

Calculate the energy released in the $\beta^+$ decay of $^{22}\textrm{Na}$ , the equation for which is given in the text. The masses of $^{22}\textrm{Na}$ and $^{22}\textrm{Ne}$ are 21.994434 u and 21.991383 u, respectively.

(a) Write the complete $\beta^+$ equation for ${}^{11}\textrm{C}$. (b) Calculate the energy released in the decay. The masses of ${}^{11}\textrm{C}$ and ${}^{11}\textrm{B}$ are $11.011433\textrm{ u}$ and $11.009305\textrm{ u}$, respectively.

(a) Calculate the energy released in the $\alpha$ decay of $^{238}\textrm{U}$ (b) What fraction of the mass of a single $^{238}\textrm{U}$ is destroyed in the decay? The mass of $^{234}\textrm{Th}$ is 234.043593 u. (c) Although the fractional mass loss is large for a single nucleus, it is difficult to observe for an entire macroscopic sample of uranium. Why is this?

(a) Write the complete reaction equation for electron capture by ${}^7\textrm{Be}$. (b) Calculate the energy released.

(a) Write the complete reaction equation for electron capture by $^{15}\textrm{O}$. (b) Calculate the energy released.

An old campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1/1000 the normal amount of ${}^{14}\textrm{C}$ . Estimate the minimum age of the charcoal, noting that $2^{10}=1024$.

A $^{60}\textrm{Co}$ source is labeled 4.00 mCi, but its present activity is found to be $1.85\times 10^{7}\textrm{ Bq}$. (a) What is the present activity in mCi? (b) How long ago did it actually have a 4.00-mCi activity?

(a) Calculate the activity R in curies of 1.00 g of ${}^{226}\textrm{Ra}$. (b) Discuss why your answer is not exactly 1.00 Ci, given that the curie was originally supposed to be exactly the activity of a gram of radium.

Show that the activity of the $^{14}\textrm{C}$ in 1.00 g of $^{12}\textrm{C}$ found in living tissue is 0.250 Bq.

Mantles for gas lanterns contain thorium, because it forms an oxide that can survive being heated to incandescence for long periods of time. Natural thorium is almost 100% ${}^{232}\textrm{Th}$, with a half-life of $1.405\times 10^{10}\textrm{ y}$. If an average lantern mantle contains 300 mg of thorium, what is its activity?

Cow’s milk produced near nuclear reactors can be tested for as little as 1.00 pCi of $^{131}\textrm{I}$ per liter, to check for possible reactor leakage. What mass of $^{131}\textrm{I}$ has this activity?

(a) Natural potassium contains ${}^{40}\textrm{K}$ , which has a half-life of $1.277\times 10^{9}\textrm{ y}$. What mass of ${}^{40}\textrm{K}$ in a person would have a decay rate of 4140 Bq? (b) What is the fraction of ${}^{40}\textrm{K}$ in natural potassium, given that the person has 140 g in his body? (These numbers are typical for a 70-kg adult.)

There is more than one isotope of natural uranium. If a researcher isolates 1.00 mg of the relatively scarce $^{235}\textrm{U}$ and finds this mass to have an activity of 80.0 Bq, what is its half-life in years?

${}^{50}\textrm{V}$ has one of the longest known radioactive half-lives. In a difficult experiment, a researcher found that the activity of 1.00 kg of ${}^{50}\textrm{V}$ is 1.75 Bq. What is the half-life in years?

You can sometimes find deep red crystal vases in antique stores, called uranium glass because their color was produced by doping the glass with uranium. Look up the natural isotopes of uranium and their half-lives, and calculate the activity of such a vase assuming it has 2.00 g of uranium in it. Neglect the activity of any daughter nuclides.

A tree falls in a forest. How many years must pass before the ${}^{14}\textrm{C}$ activity in 1.00 g of the tree’s carbon drops to 1.00 decay per hour?

What fraction of the $^{40}\textrm{K}$ that was on Earth when it formed $4.5\times 10^{9}$ years ago is left today?

A 5000-Ci ${}^{60}\textrm{Co}$ source used for cancer therapy is considered too weak to be useful when its activity falls to 3500 Ci. How long after its manufacture does this happen?

Natural uranium is 0.7200% $^{235}\textrm{U}$ and 99.27% $^{238}\textrm{U}$ . What were the percentages of $^{235}\textrm{U}$ and $^{238}\textrm{U}$ in natural uranium when Earth formed $4.5\times 10^{9}$ years ago?

The $\beta^-$ particles emitted in the decay of ${}^3\textrm{H}$ (tritium) interact with matter to create light in a glow-in-the-dark exit sign. At the time of manufacture, such a sign contains 15.0 Ci of ${}^3\textrm{H}$. (a) What is the mass of the tritium? (b) What is its activity 5.00 y after manufacture?

World War II aircraft had instruments with glowing radium- painted dials (see Figure 31.2). The activity of one such instrument was $1.0\times 10^{5}\textrm{ Bq}$ when new. (a) What mass of $^{226}\textrm{Ra}$ was present? (b) After some years, the phosphors on the dials deteriorated chemically, but the radium did not escape. What is the activity of this instrument 57.0 years after it was made?

(a) The ${}^{210}\textrm{Po}$ source used in a physics laboratory is labeled as having an activity of $1.0\textrm{ }\mu\textrm{Ci}$ on the date it was prepared. A student measures the radioactivity of this source with a Geiger counter and observes 1500 counts per minute. She notices that the source was prepared 120 days before her lab. What fraction of the decays is she observing with her apparatus? (b) Identify some of the reasons that only a fraction of the α s emitted are observed by the detector.

Armor-piercing shells with depleted uranium cores are fired by aircraft at tanks. (The high density of the uranium makes them effective.) The uranium is called depleted because it has had its $^{235}\textrm{U}$ removed for reactor use and is nearly pure $^{238}\textrm{U}$. Depleted uranium has been erroneously called non-radioactive. To demonstrate that this is wrong: (a) Calculate the activity of 60.0 g of pure $^{238}\textrm{U}$. (b) Calculate the activity of 60.0 g of natural uranium, neglecting the $^{234}\textrm{U}$ and all daughter nuclides.

The ceramic glaze on a red-orange Fiestaware plate is $\textrm{U}_2\textrm{O}_3$ and contains 50.0 grams of ${}^{238}\textrm{U}$, but very little ${}^{235}\textrm{U}$. (a) What is the activity of the plate? (b) Calculate the total energy that will be released by the ${}^{238}\textrm{U}$ decay. (c) If energy is worth 12.0 cents per $\textrm{kW}\cdot\textrm{h}$, what is the monetary value of the energy emitted? (These plates went out of production some 30 years ago, but are still available as collectibles.)

Large amounts of depleted uranium ($^{238}\textrm{U}$) are available as a by-product of uranium processing for reactor fuel and weapons. Uranium is very dense and makes good counter weights for aircraft. Suppose you have a 4000-kg block of $^{238}\textrm{U}$. (a) Find its activity. (b) How many calories per day are generated by thermalization of the decay energy? (c) Do you think you could detect this as heat? Explain.

The Galileo space probe was launched on its long journey past several planets in 1989, with an ultimate goal of Jupiter. Its power source is 11.0 kg of ${}^{238}\textrm{Pu}$ , a by-product of nuclear weapons plutonium production. Electrical energy is generated thermoelectrically from the heat produced when the 5.59-MeV $\alpha$ particles emitted in each decay crash to a halt inside the plutonium and its shielding. The half-life of ${}^{238}\textrm{Pu}$ is 87.7 years. (a) What was the original activity of the ${}^{238}\textrm{Pu}$ in becquerel? (b) What power was emitted in kilowatts? (c) What power was emitted 12.0 y after launch? You may neglect any extra energy from daughter nuclides and any losses from escaping $\gamma$ rays.

A nuclear physicist find $1.0\textrm{ }\mu\textrm{g}$ of ${}^{236}\textrm{U}$ in a piece of uranium ore and assumes it is primordial since its half-life is $2.3\times 10^{7}\textrm{ y}$. (a) Calculate the amount of ${}^{236}\textrm{U}$ that would had to have been on Earth when it formed $4.5\times 10^{9}\textrm{ y}$ ago for $1.0 \textrm{ }\mu\textrm{g}$ to be left today. (b) What is unreasonable about this result? (c) What assumption is responsible?

Natural uranium is 0.7200% $^{235}\textrm{U}$, 99.27% $^{238}\textrm{U}$, and 0.0055% $^{234}\textrm{U}$. (a) What were the percentages of $^{235}\textrm{U}$, $^{238}\textrm{U}$, and $^{234}\textrm{U}$ in natural uranium when Earth formed $4.5\times 10^{9}$ years ago? (b) What is unreasonable about this result? (c) What assumption is responsible? (d) Where does $^{234}\textrm{U}$ come from if it is not primordial?

The manufacturer of a smoke alarm decides that the smallest current of $\alpha$ radiation he can detect is $1.00\textrm{ }\mu\textrm{A}$ . (a) Find the activity in curies of an $\alpha$ emitter that produces a $1.00\textrm{ }\mu\textrm{A}$ current of $\alpha$ particles. (b) What is unreasonable about this result? (c) What assumption is responsible?

$^2\textrm{H}$ is a loosely bound isotope of hydrogen. Called deuterium or heavy hydrogen, it is stable but relatively rare—it is 0.015% of natural hydrogen. Note that deuterium has Z = N , which should tend to make it more tightly bound, but both are odd numbers. Calculate BE/A , the binding energy per nucleon, for $^2H$ and compare it with the approximate value obtained from the graph in Figure 31.27.

${}^{56}\textrm{Fe}$ is among the most tightly bound of all nuclides. It is more than 90% of natural iron. Note that ${}^{56}\textrm{Fe}$ has even numbers of both protons and neutrons. Calculate $\dfrac{\textrm{BE}}{\textrm{A}}$ , the binding energy per nucleon, for ${}^{56}\textrm{Fe}$ and compare it with the approximate value obtained from the graph in Figure 31.27.

$^{209}\textrm{Bi}$ is the heaviest stable nuclide, and its BE / A is low compared with medium-mass nuclides. Calculate BE/A , the binding energy per nucleon, for $^{209}\textrm{Bi}$ and compare it with the approximate value obtained from the graph in Figure 31.27.

(a) Calculate $\dfrac{\textrm{BE}}{\textrm{A}}$ for ${}^{235}\textrm{U}$ , the rarer of the two most common uranium isotopes. (b) Calculate BE / A for ${}^{238}\textrm{U}$. (Most of uranium is ${}^{238}\textrm{U}$.) Note that ${}^{238}\textrm{U}$ has even numbers of both protons and neutrons. Is the $\dfrac{\textrm{BE}}{\textrm{A}}$ of ${}^{238}\textrm{U}$ significantly different from that of ${}^{235}\textrm{U}$ ?

(a) Calculate BE / A for $^{12}\textrm{C}$. Stable and relatively tightly bound, this nuclide is most of natural carbon. (b) Calculate BE / A for $^{14}\textrm{C}$. Is the difference in BE / A between $^{12}\textrm{C}$ and $^{14}\textrm{C}$ significant? One is stable and common, and the other is unstable and rare.

The fact that BE / A is greatest for $A$ near 60 implies that the range of the nuclear force is about the diameter of such nuclides. (a) Calculate the diameter of an $A = 60$ nucleus. (b) Compare BE / A for ${}^{58}\textrm{Ni}$ and ${}^{90}\textrm{Sr}$ . The first is one of the most tightly bound nuclides, while the second is larger and less tightly bound.

The purpose of this problem is to show in three ways that the binding energy of the electron in a hydrogen atom is negligible compared with the masses of the proton and electron. (a) Calculate the mass equivalent in u of the 13.6-eV binding energy of an electron in a hydrogen atom, and compare this with the mass of the hydrogen atom obtained from Appendix A. (b) Subtract the mass of the proton given in Table 31.2 from the mass of the hydrogen atom given in Appendix A. You will find the difference is equal to the electron’s mass to three digits, implying the binding energy is small in comparison. (c) Take the ratio of the binding energy of the electron (13.6 eV) to the energy equivalent of the electron’s mass (0.511 MeV). (d) Discuss how your answers confirm the stated purpose of this problem.

A particle physicist discovers a neutral particle with a mass of 2.02733 u that he assumes is two neutrons bound together. (a) Find the binding energy. (b) What is unreasonable about this result? (c) What assumptions are unreasonable or inconsistent?

Derive an approximate relationship between the energy of $\alpha$ decay and half-life using the following data. It may be useful to graph the log of $t_{1/2}$ against $E_\alpha$ to find some straight-line relationship.

Nuclide	$E_\alpha$ (MeV)	$t_{1/2}$
$^{216}\textrm{Ra}$	9.5	0.18 $\mu\textrm{s}$
$^{194}\textrm{Po}$	7.0	0.7 s
$^{240}\textrm{Cm}$	6.4	27 d
$^{236}\textrm{Ra}$	4.91	1600 y
$^{232}\textrm{Th}$	4.1	$1.4 \times 10^{10}\textrm{ y}$

A 2.00-T magnetic field is applied perpendicular to the path of charged particles in a bubble chamber. What is the radius of curvature of the path of a 10 MeV proton in this field? Neglect any slowing along its path.

(a) Write the decay equation for the α decay of $^{235}\textrm{U}$. (b) What energy is released in this decay? The mass of the daughter nuclide is 231.036298 u. (c) Assuming the residual nucleus is formed in its ground state, how much energy goes to the $\alpha$ particle?

The relatively scarce naturally occurring calcium isotope ${}^{48}\textrm{Ca}$ has a half-life of about $2\times 10^{16}\textrm{ y}$. (a) A small sample of this isotope is labeled as having an activity of 1.0 Ci. What is the mass of the ${}^{48}\textrm{Ca}$ in the sample? (b) What is unreasonable about this result? (c) What assumption is responsible?

A physicist scatters $\gamma$ rays from a substance and sees evidence of a nucleus $7.5\times 10^{-13}\textrm{ m}$ in radius. (a) Find the atomic mass of such a nucleus. (b) What is unreasonable about this result? (c) What is unreasonable about the assumption?

A frazzled theoretical physicist reckons that all conservation laws are obeyed in the decay of a proton into a neutron, positron, and neutrino (as in $\beta^+$ decay of a nucleus) and sends a paper to a journal to announce the reaction as a possible end of the universe due to the spontaneous decay of protons. (a) What energy is released in this decay? (b) What is unreasonable about this result? (c) What assumption is responsible?

A nucleus is observed to emit a γ ray with a frequency of $6.3\times 10^{19}\textrm{ Hz}$. What must happen to the nucleus as a consequence?

1. The nucleus must gain 0.26 MeV.
2. The nucleus must also emit an α particle of energy 0.26 MeV in the opposite direction.
3. The nucleus must lose 0.26 MeV.
4. The nucleus must also emit a β particle of energy 0.26 MeV in the opposite direction.

A uranium nucleus emits an α particle. Assuming charge is conserved, the resulting nucleus must be

1. thorium
2. plutonium
3. radium
4. curium

A typical carbon nucleus contains 6 neutrons and 6 protons. The 6 protons are all positively charged and in very close proximity, with separations on the order of $10^{-15}$ meters, which should result in an enormous repulsive force. What prevents the nucleus from dismantling itself due to the repulsion of the electric force?

1. The attractive nature of the strong nuclear force overpowers the electric force.
2. The weak nuclear force barely offsets the electric force.
3. Magnetic forces generated by the orbiting electrons create a stable minimum in which the nuclear charged particles reside.
4. The attractive electric force of the surrounding electrons is equal in all directions and cancels out, leaving no net electric force.

A nucleus in an excited state undergoes $\gamma$ decay, losing 1.33 MeV when emitting a $\gamma$ ray. In order to conserve energy in the reaction, what frequency must the $\gamma$ ray have?

$^{241}_{95}\textrm{Am}$ is commonly used in smoke detectors because its $\alpha$ decay process provides a useful tool for detecting the presence of smoke particles. When $^{241}_{95}\textrm{Am}$ undergoes $\alpha$ decay, what is the resulting nucleus? If $^{241}_{95}\textrm{Am}$ were to undergo $\beta$ decay, what would be the resulting nucleus? Explain each answer.

A $^{}{14}_6\textrm{C}$ nucleus undergoes a decay process, and the resulting nucleus is ${}^{14}_7\textrm{N}$. What is the value of the charge released by the original nucleus?

1. +1
2. 0
3. -1
4. -2

Explain why the overall charge of the nucleus is increased by +1 during the $\beta$ decay process.

Identify the missing particle based upon conservation principles:

${}^{14}_7\textrm{N} + {}^4_2\textrm{He} \rightarrow \textrm{X}+{}^{17}_8\textrm{O}$

1. ${}^2_1\textrm{H}$
2. ${}^1_1\textrm{H}$
3. ${}^{12}_6\textrm{C}$
4. ${}^{14}_6\textrm{C}$
5. ${}^8_4\textrm{Be}$

Are the following reactions possible? For each, explain why or why not.

1. $\textrm{U} \to \textrm{Ra} + \textrm{He}$
2. $\textrm{Ra} \to \textrm{Pb} + \textrm{C}$
3. $\textrm{C} \to \textrm{N} + e^- + \bar{\nu_e}$
4. $\textrm{Mg} \to \textrm{Na} + e^+ + \nu_e$

A radioactive sample has N atoms initially. After 3 half- lives have elapsed, how many atoms remain?

1. N/3
2. N/6
3. N/8
4. N/27

When Po decays, the product is Pb. The half-life of this decay process is 1.78 ms. If the initial sample contains $3.4\times 10^{17}$ parent nuclei, how many are remaining after 35 ms have elapsed? What kind of decay process is this (alpha, beta, or gamma)?

Binding energy is a measure of how much work must be done against nuclear forces in order to disassemble a nucleus into its constituent parts. For example, the amount of energy in order to disassemble He into 2 protons and 2 neutrons requires 28.3 MeV of work to be done on the nuclear particles. Describe the force that makes it so difficult to pull a nucleus apart. Would it be accurate to say that the electric force plays a role in the forces within a nucleus? Explain why or why not.