Question
What fraction of the that was on Earth when it formed years ago is left today?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 31, Problem 55 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
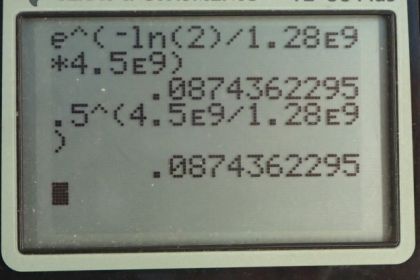
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Four and a half billion years ago when the Earth was formed it was composed of a certain amount of potassium-40 isotope and we want to figure out, what fraction of that is remaining today? So we know the half-life of potassium-40 is 1.28 billion years and we'll use this formula number 36 from chapter 31 to solve the question but then I have an alternative method down here using this one-half to the power of t over t one-half here. I'll explain what that is in a second, it's an alternative method. So the number of atoms of a radioactive material is the initial number of atoms times e to the negative decay constant times t and then we can divide these two to get the fraction of the atoms that still remain. And so we have to substitute for lambda; it's logarithm of 2 divided by the half-life; that's equation 37 and then substitute that in for lambda here and so the fraction of potassium-40 remaining is e to the negative logarithm of 2 times t over t one-half. So t one-half for potassium-40 is 1.28 times 10 to the 9 years and the Earth is 4.5 times 10 to the 9 years old and multiply that by logarithm 2 and raise e to the negative of that and we get 0.087. So there is 8.7 percent of the potassium-40 is still remaining in the Earth. An alternative method would be to say that the number of atoms equals the original number of atoms multiplied by one-half to the power of the number of half-lives that have elapsed. And so when you go an amount of time divided by the half-life, this gives you the number of half-lives, the number of times that one should multiply N naught by a half. And so we divide both sides by N naught and we get N over N naught is a half to the power of 4.5 times 10 to the 9 years divided by 1.28 times 10 to the 9 years and this also gives 0.087 as we expect.