OpenStax College Physics for AP® Courses, Chapter 31, Problem 54 (Problems & Exercises)

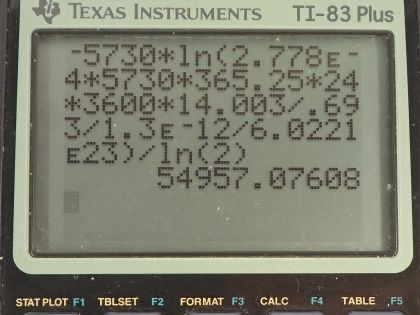
This is College Physics Answers with Shaun Dychko. A tree falls in a forest and we assume that in some future time, 1.00 gram of carbon will be harvested from this tree and its activity will be measured and it will be 1.00 decay per hour which I convert into becquerels by multiplying by 1 hour for every 3600 seconds and we want to know in how long will this activity of the carbon in 1.00 gram of carbon be down to 1.00 decay per hour? So it's only the carbon-14 that is undergoing decay and so we know the ratio of carbon-14 to carbon in general, which is 1.3 times 10 to the minus 12 and there's an assumption that this ratio is constant over many thousands of years, which is a reasonable assumption because carbon-14 is being produced in the atmosphere continuously by neutrinos interacting with nitrogen— neutrinos from the Sun. So this is the ratio of carbon-14 to carbon in general, the carbon-14 half-life is 5730 years and the molar mass of carbon-14 is 14.003 grams per mol. So that's the information we need to answer this question: in how long will the activity of 1.00 gram of carbon that was created in organic life form today will have an activity of 1.00 decay per hour? So activity of some future time is the original activity times e to the negative λt and we can divide both sides by R naught and get e to the λt is R over R naught, and then take the natural logarithm of both sides which gives us negative λt equals natural logarithm of the future activity divided by the original activity. λ is natural logarithm of 2 divided by the half-life and so we can substitute that in and then multiply both sides by t one-half over ln of 2 and negative by the way and then we get t is negative of the half-life times natural logarithm of R over R naught divided by natural logarithm of 2. So the tree part here is to figure out what is this R naught— this original activity— so what activity does the carbon-14 in 1 gram of carbon overall have today? Well that original activity will be 0.693 times the original number of atoms of carbon-14 divided by its half-life and the number of atoms is going to be the mass of carbon-14 divided by the molar mass of carbon-14 multiplied by Avogadro's number and then we substitute all that in here for N naught and then the mass of carbon-14 is going to be 1.3 times 10 to the minus 12 times the mass of carbon in general rearranging this ratio here by multiplying both sides by mass of carbon and so we get the mass of carbon-14 is mc times this ratio 1.3 times 10 to the minus 12 so that substitute was done here and all of this gets plugged in for R naught in our formula for t I am going to... since we are dividing by R naught, I am going to multiply by the reciprocal of R naught and so we have the original activity times half-life of carbon-14 times molar mass of carbon-14 divided by 0.693 times the mass of carbon times 1.3 times 10 to the minus 12 times Avogadro's number and otherwise, this formula is the same as what we had up here. Then we plug in numbers. And so that's negative 5730 years— and by choosing years as units for this factor here, our answer will be in units of years as well— and we multiply by natural logarithm of the original activity, which is 2.778 times 10 to the minus 4 becquerels— that's 1.00 decay per hour converted into decays per second or otherwise known as becquerels— and then multiply by the half-life but this time, I don't leave it in years and this time I have to convert it into seconds in order to work with the becquerels here. So we multiply this half-life of carbon-14 by 365.25 days per year times 24 hours per day times 3600 seconds per hour and then multiply by the molar mass— 14.003 grams per mol— and divide by 0.693 times 1.00 gram of carbon that was harvested from the tree times 1.3 times 10 to the minus 12 to figure out the mass of the carbon-14 isotope times 6.0221 times 10 to the 23 atoms per mol divided by natural log of 2 and that is 55000 years. So in 55000 years, 1.00 gram of carbon taken from this tree will have an activity of 1.00 decay per hour.