Question
A rare decay mode has been observed in which emits a nucleus. (a) The decay equation is . Identify the nuclide . (b) Find the energy emitted in the decay. The mass of is .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 31, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
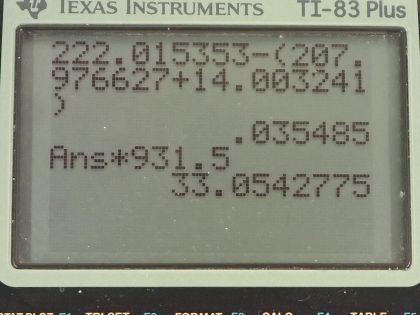
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Radium sometimes decays to produce carbon-14 and the question is what is this other nuclide that it will produce, what other daughter nuclide is made from this parent nuclide? So the total number of nucleons has to be the same on both sides of this equation and so A is going to be the total of 222 minus the 14 accounted for in the carbon-14 for 208 leftover. Now with 88 protons in radium, which we can look up in this appendix here number 88 is radium and 6 are used up in the carbon nuclide that leaves 82 leftover for this thing and so this is lead because lead has an atomic number of 82, it's lead-208 which is the most common isotope for lead. So the full equation then is radium-222 decays into lead-208 plus carbon-14. Part (b) is asking what energy is released? So what we want to know is what is the mass difference between the two sides of this equation and we multiply that change in mass by c squared. We are going to use atomic masses from this data table here and the atomic masses include the mass of the electrons that surround the nucleus and that's okay because we have an equal number of electrons on the left and right side of this equation and so they subtract out... just it's a wash because you know you have 222 electrons included in this atomic mass and you will have 222 electrons included in the atomic mass total of carbon-14 and lead-208. Okay! So we look up these masses in the data table and we get 222.015353 atomic mass units for radium-222 and from that, we subtract the total atomic masses of lead-208 and carbon-14 and we are left with 0.035485 atomic mass units and then we multiply that by 931.5 megaelectron volts per c squared for every atomic mass unit and the atomic mass units cancel this c squared from the E equals mc squared formula cancels with the c squared in the denominator of these units and we are left with megaelectron volts and that is 33.05 megaelectron volts released.