Question
(a) Show that if you assume the average nucleus is spherical with a radius , and with a mass of , then its density is independent of .
(b) Calculate that density in and , and compare your results with those found in Example 31.1 for .
Final Answer
- Please see the solution video for the derivation.
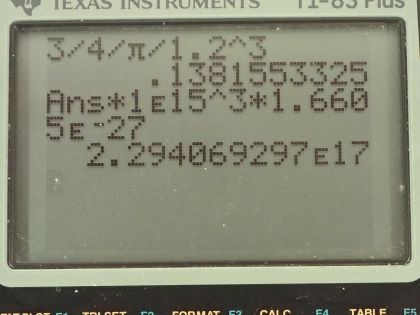
- or . This is the same as in Example 31.1.
Solution video
OpenStax College Physics for AP® Courses, Chapter 31, Problem 14 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The radius of a nucleus is this r naught multiplied by its mass number to the power of one-third and the mass of a nucleus we'll assume is equal to the mass number and in part (a), we'll assume the nucleus is a sphere and figure out its density and show that the density is independent of A; it doesn't matter what the mass number is, the density will be the same regardless. So the volume for a sphere then is four-thirds π times the radius cubed so we can substitute that in for V here in this density formula density of course is mass per volume and when we divide by this, we are going to multiply by its reciprocal which is 3 over 4πr cubed. So we have 3m over 4πr cubed is the density. Now r, we can make a substitution for it with this formula here and we'll replace r with r naught times A to the power of one-third and then in the next step here, we'll replace m with A atomic mass units so the units are u and the factor is A and I have also applied this exponent to both the factors in this bracket here so we have r naught cubed and A to the one-third cubed and then we replaced m with A atomic mass units. So this A cancels with this A because A to the one-third cubed is A to the power of 1 and we are left with 3 atomic mass units divided by 4π times r naught cubed is the density and the letter A does not appear anywhere in this formula and so density is independent of A. Part (b) says calculate the density in units of atomic mass units per cubic femtometer and also in kilograms per cubic meter. So we have this formula for density that we found in part (a) and so we'll plug in 1.2 femtometers in place of r naught so we have 3 atomic mass units divided by 4π times 1.2 femtometers cubed and that is 0.138 atomic mass units per cubic femtometer. Then we'll convert this into kilograms per cubic meter by multiplying by 10 to the 15 femtometers per meter 3 times and that will cancel the femtometers cubed leaving us with meters cubed on the bottom and then we multiply by 1.6605 times 10 to the minus 27 kilograms per atomic mass unit and we have 2.29 times 10 to the 17 kilograms per cubic meter. This is the same density as example 31.1.