Question
56Fe{}^{56}\textrm{Fe} is among the most tightly bound of all nuclides. It is more than 90% of natural iron. Note that 56Fe{}^{56}\textrm{Fe} has even numbers of both protons and neutrons. Calculate BEA\dfrac{\textrm{BE}}{\textrm{A}} , the binding energy per nucleon, for 56Fe{}^{56}\textrm{Fe} and compare it with the approximate value obtained from the graph in Figure 31.27.
<b>Figure 31.27</b> A graph of average binding energy per nucleon, BE / A , for stable nuclei. The most tightly bound nuclei are those with A near 60, where the attractive nuclear force has its greatest effect. At higher A s, the Coulomb repulsion progressively reduces the binding energy per nucleon, because the nuclear force is short ranged. The spikes on the curve are very tightly bound nuclides and indicate shell closures.
Figure 31.27 A graph of average binding energy per nucleon, BE / A , for stable nuclei. The most tightly bound nuclei are those with A near 60, where the attractive nuclear force has its greatest effect. At higher A s, the Coulomb repulsion progressively reduces the binding energy per nucleon, because the nuclear force is short ranged. The spikes on the curve are very tightly bound nuclides and indicate shell closures.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

8.790 MeV/nucleon8.790\textrm{ MeV/nucleon}
Yes, this approximately agrees with the binding energy per nucleon shown on the graph.

Solution video

OpenStax College Physics for AP® Courses, Chapter 31, Problem 70 (Problems & Exercises)

OpenStax College Physics, Chapter 31, Problem 70 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

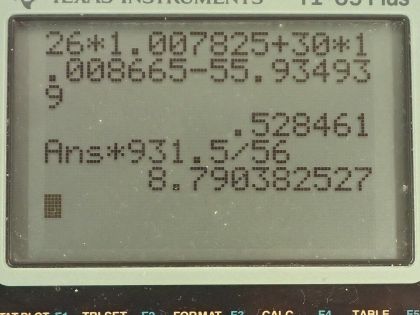
Calculator Screenshots

  • OpenStax College Physics, Chapter 31, Problem 70 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the binding energy per nucleon in iron-56 In the appendix at the end of the textbook. we can see that the atomic mass is 55.934939 atomic mass units for a single iron-56 atom and the atomic number for iron is 26, which means it has 26 protons and then 56 minus 26 gives us 30 neutrons. So the binding energy per nucleon is the mass defect which is the difference in mass between the nucleons in their free independent states minus the atomic mass of this iron atom with all the nucleons bound together and then we divide that by the number of nucleons, which is 56 and then multiply by c squared to get the amount of energy per nucleon. So the mass defect or this mass difference between the free nucleons versus their bound state is 26 times the atomic mass of hydrogen and this mass includes 26 electrons but that's okay because we are going to be subtracting away the mass of 26 electrons in this atomic mass for iron, which also includes 26 electrons. Okay! So we have 26 times the atomic mass of hydrogen plus 30 times the mass of free neutrons and then subtract away from that the atomic mass of iron and this gives 0.528461 atomic mass units. We want to keep lots of digits here because the differences tend to be quite small so use lots of digits to do your calculations. So the binding energy per nucleon then is this mass defect converted into megaelectron volts per c squared by multiplying by 931.5 for every atomic mass unit and then the c squared's cancel here giving us an answer in megaelectron volts and we divide the numerator by 56— the number of nucleons— and we get 8.790 megaelectron volts of binding energy per nucleon. The question asks us to compare our answer to what we would expect based on the graph and so when we find iron approximately here and move horizontally to see where that lines up on this vertical axis, we can see that's slightly below 9 so yeah our answer approximately agrees with what we would expect by looking at this graph.