Question
A nucleus in an excited state undergoes decay, losing 1.33 MeV when emitting a ray. In order to conserve energy in the reaction, what frequency must the ray have?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 31, Problem 4 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
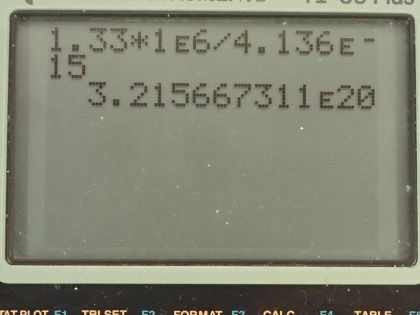
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A nucleus undergoes gamma-decay and it loses 1.33 megaelectron volts in the process so that means the energy of the gamma ray must be this energy because that's where the energy goes that the nucleus has lost. So what is the frequency of this gamma ray then? Well we know the energy of a photon is Planck's constant multiplied by the frequency so we divide both sides by Planck's constant to solve for f and it's the energy divided by h. So that's 1.33 megaelectron volts times 1 times 10 to the 6 electron volts for every megaelectron volt and then we divide by Planck's constant written with units of electron volt seconds and then we'll end up with reciprocal seconds as our units here, which is hertz. So we are dividing by 4.136 times 10 to the negative 15 electron volt seconds and that gives a frequency of 3.22 times 10 to the 20 hertz.