Question
An old campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1/1000 the normal amount of . Estimate the minimum age of the charcoal, noting that .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 31, Problem 44 (Problems & Exercises)
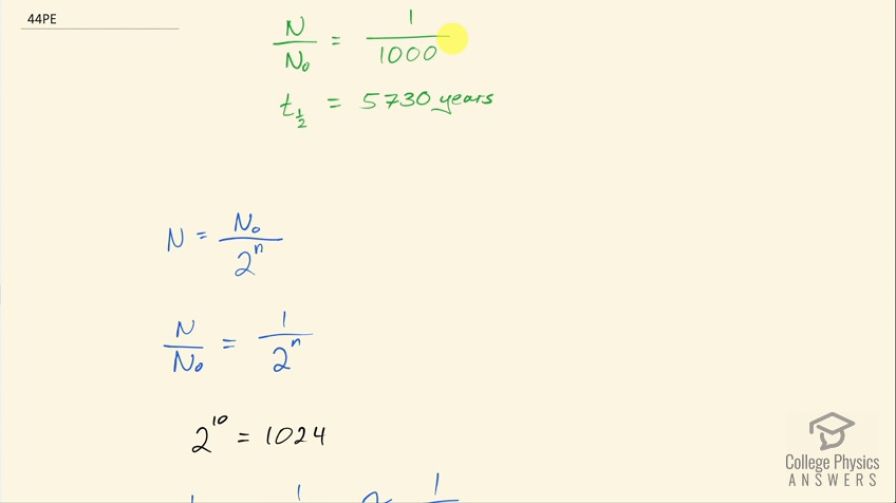
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. An old campfire has been discovered and it was used to burn some sort of organic matter some time ago maybe some wood from trees or other organic matter... whatever it was, it had carbon-14 in it and we are told that there is 1 one-thousandth as much carbon-14 now as you would expect in a living tissue now and this is because after the organic matter died and was burned in the campfire, the refreshing of its carbon didn't occur anymore there's no carbon exchange with the environment anymore it didn't have any carbon-14 uptake anymore and so whatever carbon-14 it had at the time that it was burned has been decaying since then to the point where now there's 1 one-thousandth of the amount that it originally had. So the half-life of carbon-14 is 5730 years and I looked that up in appendix B right here and we know that the number of carbon-14 atoms now equals the number that it had originally divided by 2 to the power of little n, where little n is the number of times we should divide by 2 and we divide by 2 each time a period of a half-life has passed. So after 5730 years, divide by 2 once and then by this amount of time yet again divide by 2 again so this little n is a thing we have to solve for— it will tell us how many half-lives have passed— and then we'll convert that into number of years by multiplying by 5730 years per half-life. So let's multiply both sides by 1 over N naught— the original number of carbon-14 atoms— and that gives us this ratio equals 1 over 2 to the power of n. We are told to estimate in this question, which means we won't use our calculator and we are also told that 2 to the power of 10 is 1024. So 1 over 2 to the n is this ratio N over N naught and that is 1 one-thousandth and this is approximately the same as 1 over 1024—close enough anyway for an estimate— so we'll say that the number 10 is the exponent for 2 in order to make 1 one-thousandth. So that means the amount of time passed then is number of half lives times the half-life. So that's 10 half-lives approximately times 5730 years per half-life and that is 57000 years.