Question
To get an idea of the small effect that temperature has on Archimedes’ principle, calculate the fraction of a copper block’s weight that is supported by the buoyant force in water and compare this fraction with the fraction supported in water.
Final Answer
The ratio of the buoyant force to the copper weight is greater at than at by a factor of .
Solution video
OpenStax College Physics for AP® Courses, Chapter 13, Problem 67 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
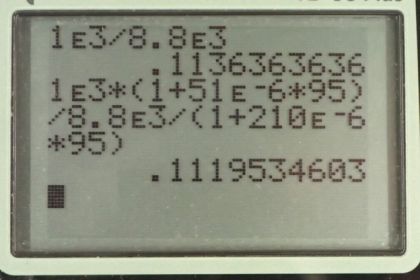
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. So a piece of Copper is submerged within some water and we're going to calculate the ratio of the buoyant force provided by the water divided by the weight of the Copper. So what fraction of its weight is supported by the buoyant force? So, buoyant force is going to be the weight of water displaced by the Copper. And that's going to be the mass of water displaced times g which is going to be the density of water times the volume of water displaced which I've written as V subscript c here and not w because the volume of water displaced is going to equal the volume of Copper that is submerged. And so we have rho w density of water times Vc, volume of Copper times g, because density by the way is mass divided by volume and so if we want mass which is what this factor is here, we multiplied both sides by V and its volume times density which we've written here. So, the buoyant force divided by the weight of the Copper is going to be buoyant force divided by mass of Copper times g. And the mass of Copper is going to be the density of Copper times the volume of the Copper, basically with the same argument as here. And then we'll substitute in this buoyant force that we calculated here rho wVcg and we see that the Vc and the g are common factors so the top and bottom should be cancel. And so the ration of the buoyant force to the weight of the Copper is going to be the ratio of their densities, density of water divided by density of Copper. And at about zero degrees Celsius, that is approximately one times ten to the three kilograms per cubic meter for water. And then for Copper, it's 8.8 times ten to three kilograms per cubic meter. And we get a ratio of about 0.114. So the buoyant force is about 11.4 percent of the weight of the Copper. Now, at 95 degrees Celsius, things will change a little bit because the volumes are going to change, so the Copper will expand because it's now at higher temperature and the water also will expand due to this increase in temperature to 95 degrees Celsius. And if the expansions were the same, then the ratio of the buoyant force to the weight would not change but as we'll see, the expansions are not the same, they have different volume coefficients of expansion. This beta factor here. So, now in this case I have a prime here to denote that we're dealing with variables that are at 95 degrees Celsius instead of zero. And so the buoyant force prime, divided the weight of the Copper which doesn't change. At which temperature, it's still the same mass there equals the new density of water divided by the new density of Copper, even though the weight of the Copper does not change, its density does change because its volume won't be changing. So, the new density of either of this materials is going to be whatever mass it had before divided by the new volume. And the new volume is going to be the old volume multiplied by one plus this volume coefficient of expansion times the change in temperature. And this old mass divided by old volume is just the original density. And so we have rho divided by one plus beta delta T. So, we're going to substitute this into this. And so we have density of water prime at 95 degree Celsius it's going to be the density of water at zero divided by one plus the coefficient of expansion of water times the change in temperature. And we're going to divide that by this density of Copper at 95 degrees Celsius, but we're not going to divide this fraction by a fraction, because it's messy, so I'm instead going to multiply by the reciprocal of this new density of Copper. And the reciprocal is going to be this one plus volume coefficient of expansion for Copper times change in temperature divided by the original density of Copper. And so we end up with this expression here, when you just move the factors around a little bit and we have that the ratio of the new densities is going to be the old density of water times one plus the volume coefficient of expansion for Copper of 51 times ten to the minus six per Celsius degree times the change in temperature which is 95 Celsius degrees divided by the density of Copper, 8.8 times ten to the three kilograms per cubic meter times one plus the volume coefficient of expansion for water, 210 times ten to the minus six and then that's times by 95 Celsius degrees change in temperature and we get 0.112 now. And so we take these, the first ratio divided the second ratio. And so that's 0.11364 divided by 0.11195 when you don't round it and that gets 1.02. So the ratio of the buoyant force to the Copper weight is greater at zero degrees Celsius than at 95 degrees Celsius by a factor of 1.02. And we expected this to change, I mean if it was 1.00 then there would have been no change and we expected the coefficient or the ratio to be less at a higher temperature because the water expands more due to a greater volume coefficient of expansion. And so, the weight of the water displaced is going to be less since the water being displaced is now of lower density. And despite more water being displaced as a result of the Copper expanding, since the Copper does not expand as much, the balance of factors results in a net less weight of water displaced in solving for less buoyant force.