OpenStax College Physics for AP® Courses, Chapter 13, Problem 13 (Problems & Exercises)

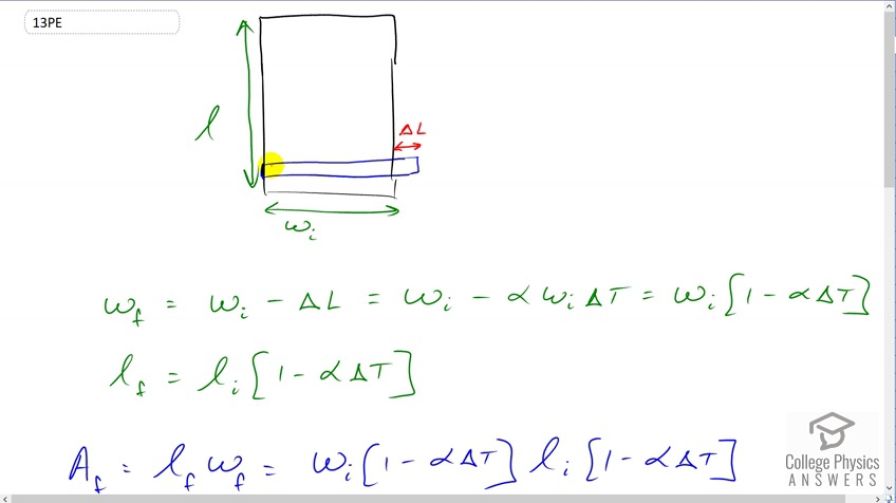
This is College Physics Answers with Shaun Dychko. This rectangle represents the parcel of land in the very expensive city of Hong Kong. This blue rectangle is the steel tape measure. So when the temperature goes up by 20 degrees Celsius, or 20 Celsius degrees I suppose we're meant to say, the tape measure will expand by this amount delta l. When it does that some smaller numbers here will now line up with the edge of the parcel. So it's going to give a measurement that is smaller after the tape measure has expanded than it did before. So initially we'll say that it measured the length of w i for initial, and then the final width that it measures after the 20 Celsius degree increase in temperature will be the initial width minus this portion by which the steel tape measure has expanded or lengthened. So this delta l is going to be the coefficient of linear expansion for steel times the initial width, times the change in temperature. We can factor out this w i from both terms and we get the final width will be the initial width times one minus alpha delta t. The same sort of thing can be shown for the final length will be the initial length times one minus alpha delta t as well. Now the final area that will be calculated then is going to be the final length times the final width, and then substituting for each of those here we can see that there is this one minus alpha delta t factor that is in both of these factors here. So it becomes squared. So we have the final area will be the initial area basically, times one minus alpha delta t squared. Now the change in area is what's interesting here because we're wanting to find the change in the cost. That's going to be the dollars per square meter times the change in area. So we have the final area minus the initial area and that's going to be w i l i times one minus alpha delta t squared minus w i l i which is the initial area. We can factor out this w i l i from both terms. So we get the change in area is initial width times initial length times one minus alpha delta t squared, minus one. So then we take all of that and multiply it by the cost per square meter and we get our answer. So the change in cost will be 60 thousand dollars per square meter times 20 meters times 30 meters, the initial width and length measurements, times one minus 12 times ten to the minus six, coefficient of linear expansion for steel, times the change in temperature of 20 Celsius degrees and then square all of this here, and then minus one. You get negative 17 thousand. So the price decreases by 17 thousand dollars on account of making this measurement on a hot day with a steel tape measure.