Question
(a) What is the average kinetic energy in joules of hydrogen atoms on the 5500∘C5500^\circ\textrm{C} surface of the Sun? (b) What is the average kinetic energy of helium atoms in a region of the solar corona where the temperature is 6.00×105 K6.00 \times 10^5 \textrm{ K}?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 1.20×10−19 J1.20 \times 10^{-19} \textrm{ J}
  2. 1.24×10−17 J1.24 \times 10^{-17} \textrm{ J}

Solution video

OpenStax College Physics for AP® Courses, Chapter 13, Problem 41 (Problems & Exercises)

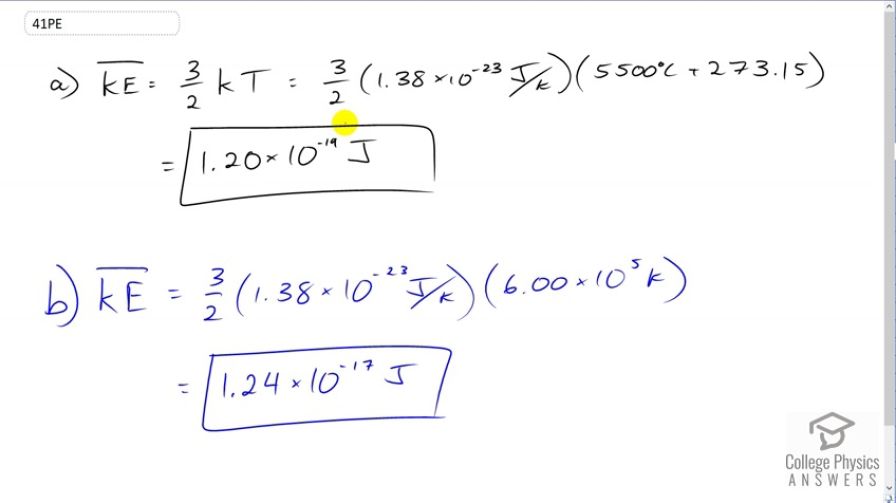
OpenStax College Physics, Chapter 13, Problem 41 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 13, Problem 41 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. Average kinetic energy is three over two times Boltzmann's constant times temperature in Kelvin. So that's three over two times 1.38 times ten to the minus twenty-three joules per Kelvin, times 5500 degrees Celsius, the surface of the sun converted into Kelvin by adding 273.15. This works out to 1.20 times ten to the minus nineteen joules. So that's the average kinetic energy of hydrogen atoms. It doesn't have to be hydrogen atoms; it could be any particle with that temperature. Now at this -- in the sun's corona where the temperature is six times ten to the five Kelvin, we multiply by Boltzmann's constant and times three over two and we get 1.24 times ten to the minus seventeen joules.