Question
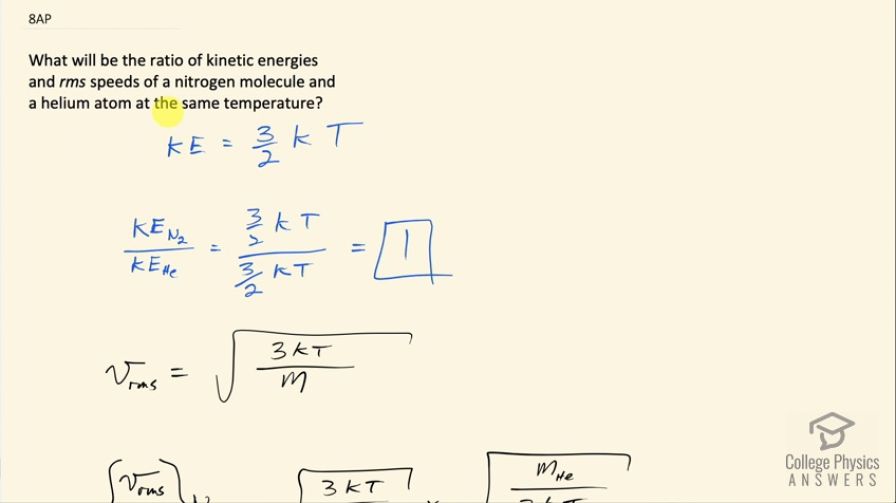
What will be the ratio of kinetic energies and rms speeds of a nitrogen molecule and a helium atom at the same temperature?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 13, Problem 8 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. What is the ratio of kinetic energies and rms speeds of a nitrogen molecule versus a helium atom at the same temperature? A nitrogen molecule is N 2— it's a diatomic molecule in the Earth's atmosphere in its natural state— and helium atom is just going to be He—one single atom. Okay! So average kinetic energy is 3 over 2 times Boltzmann's constant times the absolute temperature in Kelvin and nowhere in here does the mass appear so when we take the kinetic energy of nitrogen molecule, divide that by the average kinetic energy of a helium atom it's 3 over 2 k divided by 3 over kT— no need for any subscripts because the temperatures are the same of course it's the same Boltzmann's constant— and we end up with 1 is going to be the ratio of their kinetic energies. For the rms speed however the mass is a factor and so this ratio is not going to be one. So v rms is a square root of 3 times Boltzmann's constant times absolute temperature divided by mass. So we have v rms of a nitrogen molecule divided by v rms of helium atom, it's gonna be square root 3kT over mass of a nitrogen molecule and then instead of dividing this by a messy fraction, we are going to multiply it by the reciprocal of the denominator so that's multiplying by square root of m He over 3kT and the square root 3kT's cancel and we are left with this ratio then is the square root of the mass of a helium atom divided by mass of a nitrogen molecule. So we need to look up this data in appendix A in the textbook and nitrogen atom has an atomic mass of 14.003 atomic mass units and I suppose I should technically be taking the weighted average of the different isotopes but since 99.63 percent of nitrogen exists in this isotope, I am gonna use that number. Helium approximately 100 percent has a mass of 4.002 or 4.003 I guess atomic mass units for helium. So we take square root of 4.003 atomic mass units for Helium divided by 2 times 14.003 atomic mass units for nitrogen and it's a molecule consisting of two atoms and that's why there's a factor 2 here and we end up with 0.378 is the ratio of the rms speeds.
