Question
(a) If a 500-mL glass beaker is filled to the brim with ethyl alcohol at a temperature of 5.00∘C5.00^\circ\textrm{C} how much will overflow when its temperature reaches 22.0∘C22.0^\circ\textrm{C}? (b) How much less water would overflow under the same conditions?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 9.35 mL9.35 \textrm{ mL}
  2. 7.57 mL7.57 \textrm{ mL}
    Note: The wording of the question in part (b) is sneaky - it isn't asking for the amount of spill that would happen with water, but rather how much less spillage there would be with water. The answer in the video of 1.79 mL1.79 \textrm{ mL} is amount of spill that would happen with water, but this should be subtracted from the amount of spill with ethyl alcohol to get how much less spillage there is, which is 9.35 mL−1.785 mL=7.57 mL9.35\textrm{ mL} - 1.785\textrm{ mL} = 7.57 \textrm{ mL}. The final answer above and the calculator screenshots have been corrected but the video mistakenly says only how much spill there would be with water in part (b).

Solution video

OpenStax College Physics for AP® Courses, Chapter 13, Problem 17 (Problems & Exercises)

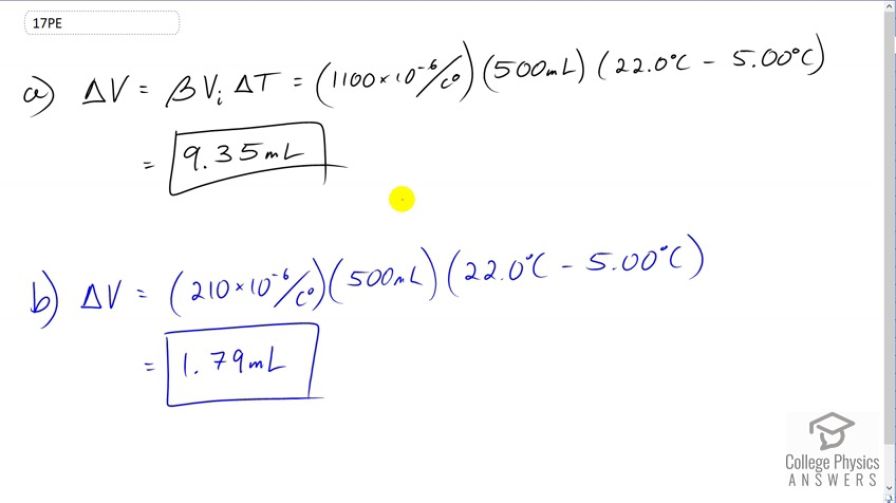
OpenStax College Physics, Chapter 13, Problem 17 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 13, Problem 17 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to assume that this ethyl Alcohol is poured into a beaker which is initially at the room temperature. So the beaker is at room temperature and the alcohol is initially at five degrees Celsius. After it sits in the beaker for a while, its temperature will increase to 22 which is room temperature. All the while, the beaker will basically stay at 22 degrees because it started at 22 degrees and the room air will keep it at 22. So that means the change in volume here, the amount of ethyl alcohol that's spills will be just due to the change in volume of the ethyl alcohol. We don't have to think about the beaker changing in volume. So we multiply the volume expansion coefficient for ethyl alcohol by its initial volume and then by the change in temperature. So that's 1100 times ten to the minus six, times 500 milliliters, times 22 degrees Celsius minus five degrees Celsius, giving 9.35 milliliters. Now if the beaker was instead filled with water and not ethyl alcohol, the only change is the expansion coefficient which will be 210 times ten to the minus six for water. That will result in a spill of volume 1.79 milliliters.