Question
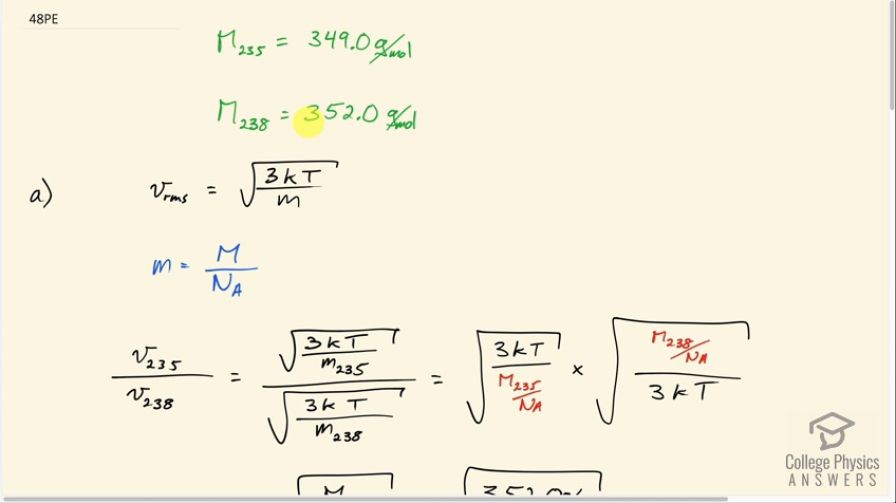
There are two important isotopes of uranium— and have different atomic masses. Only is very useful in nuclear reactors. One of the techniques for separating them (gas diffusion) is based on the different average velocities of uranium hexafluoride gas, . (a) The molecular masses for and are 349.0 g/mol and 352.0 g/mol, respectively. What is the ratio of their average velocities? (b) At what temperature would their average velocities differ by 1.00 m/s? (c) Do your answers in this problem imply that this technique may be difficult?
Final Answer
- This is a temperature that can reasonably by worked with in controlled industrial settings.
Solution video
OpenStax College Physics for AP® Courses, Chapter 13, Problem 48 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When uranium is mined out of the ground most of it consists of the uranium 238 isotope which has a molar mass of 352 grams per mole, but the isotope that's useful for nuclear reactors is uranium-235 with a molar mass of 349.0 grams per mole. So the uranium ore that's initially mined has to be enriched which is to say that they need to change the proportion of this isotope versus the 238. They have to create a mixture that has more uranium-235 in it to be useful in a nuclear reactor. So Part A says supposing you create a uranium fluoride gas and you want to know what the ratio of their average velocities will be, that's in Part A, and then at what temperature would their average velocities differ by one meter per second? Because this difference in velocity can be used to separate them using gas diffusion. So RMS speed is square root of 3 times Boltzmann's constant times absolute temperature divided by the mass of a single atom. And the mass of a single atom will be the molar mass divided by Avogadro's number although of course that'll be in grams, but that's good enough for here. That's just another conversion factor to go from grams to kilograms and we cancel in this division that we're going to do here. So we have the RMS of the 235 isotope divided by the speed of the 238 isotope will be square root 3 K T over M of 235 divided by square root of 3 K T over M 238. So we're dividing a square root of a fraction by the square root of a fraction. I'm going to instead multiply by the reciprocal of the denominator. So I'm going to multiply it; this part will go in the numerator here, but I'm making a substitution for it using this and writing the molar mass of uranium 238 divided by Avogadro's number as a substitution for the mass of a single atom, and that's divided by three K T and this being the flipped version of this because I find it less confusing to multiply by the reciprocal of something rather than divide by the fraction. So a whole bunch of things cancel. So we have square root 3 K T here and square root 3 K T in the denominator here and these Avogadro numbers cancel and we're left with the square root of the molar mass of uranium 238 divided by the molar mass of 235. So that's square root 352 grams per mole divided by 349 grams per mole and that's a ratio of 1.004. Part B says: what will the temperature be such that the difference in these RMS speeds would be 1.00 meters per second? So we make a substitution using this formula here for each of the speeds and in this case it's dividing by the mass of the 235 isotope and in this case dividing by the mass of the 238 isotope. The 235 mass will be 349 grams per mole that we're given multiplied by one kilogram for every one thousand grams. So that makes the units so far kilograms per mole and then multiplied by one mole for every 6.02 times 10 to the 23 atoms and the moles cancel giving us kilograms per atom. And that is 5.7974 times ten to the minus 25 kilograms per atom. Keeping lots of digits here because we know that the differences here are small and it doesn't hurt to keep lots of digits. And we'll do rounding with appropriate significant figures in the final answer. So for the mass of a 238 atom we have 352 grams per mole multiplying through by these conversion factors giving us 5.84718 times ten to the minus 25 kilograms per atom. So the square root 3 K T can be factored out from both of these terms and we're left with square root 3 K T times square root one over M 235 minus one over square root one over M 238 equals one meter per second. And then we'll divide both sides by this bracket. And so we have square root 3 K T is one over square root one over M 235 square root one over M 238. And then we'll square both sides and then afterwards divide by one over 3 K or multiply by one over 3 K which is the same as dividing by 3 K and that isolates T on the left side. So we have T equals 1 meter per second over this binomial and we square all that times 1 over 3 times Boltzmann's constant. So that's 1 divided by square root 1 over 5.79734 times ten to the minus 25 kilograms mass of a uranium-235 atom minus square root one over 5.84717 times ten to the minus 25 kilograms mass of a uranium 238 atom. And we square that and multiply by 1 over 3 times Boltzmann's constant giving us 768 Kelvin. And this temperature can be reasonably worked with in a controlled industrial setting and so this could be a process that's useful for enriching uranium.
