Question
Angioplasty is a technique in which arteries partially blocked with plaque are dilated to increase blood flow. By what factor must the radius of an artery be increased in order to increase blood flow by a factor of 10?
Final Answer
The radius must be increased by a factor of 1.8.
Solution video
OpenStax College Physics, Chapter 12, Problem 36 (Problems & Exercises)
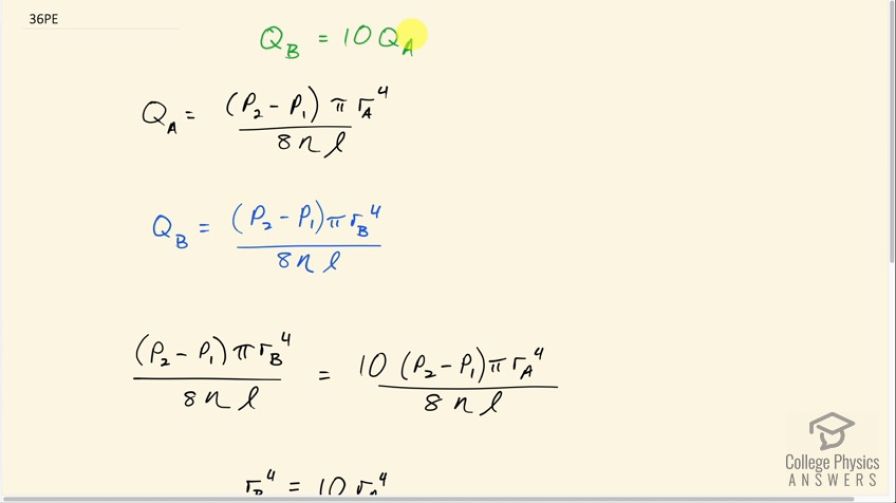
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Angioplasty is needed to increase the rate of blood flow by 10 times what it is when the blood vessel is constricted and the question here is what new radius is needed such that the flow will increase to 10 times what it was before. So in the first scenario, we have some pressure difference times pi times some radius ‘A’ to the power four divided by eight times the viscosity of blood times the length of this blood vessel. And then in scenario B, we have all the same things, all the same factors, except the radius will be radius ‘B’ and we have to figure out by what factor does radius ‘B’ increase compared to radius ‘A’. Okay, so this is flow rate ‘B’ equals 10 times flow rate ‘A’. And we can cancel all these common factors on both sides. And we’re left with r B to the power of four equals 10 times r eight to the power four. And then we can take the fourth root of both sides, which is the same as raising both sides to the exponent one quarter. And that gives us r B in the left and 10 to the power of one quarter times r A and 10 to the power quarter is 1.78. So the radius r B has to be increased by a factor of 1.8 compared to the original radius.
