Question
Every few years, winds in Boulder, Colorado, attain sustained speeds of 45.0 m/s (about 100 mi/h) when the jet stream descends during early spring. Approximately what is the force due to the Bernoulli effect on a roof having an area of 220 m2220 \textrm{ m}^2? Typical air density in Boulder is 1.14 kg/m31.14 \textrm{ kg/m}^3, and the corresponding atmospheric pressure is 8.89×104 N/m28.89 \times 10^4 \textrm{ N/m}^2. (Bernoulli's principle as stated in the text assumes laminar flow. Using the principle here produces only an approximate result, because there is significant turbulence.)
Question by OpenStax is licensed under CC BY 4.0
Final Answer

2.54×105 N2.54 \times 10^5 \textrm{ N}

Solution video

OpenStax College Physics, Chapter 12, Problem 21 (Problems & Exercises)

OpenStax College Physics, Chapter 12, Problem 21 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 12, Problem 21 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. So in Colorado we have this air moving quickly over the roof of this house and the pressure inside was going to higher because the air inside the house is not moving at all. And so, when we're looking at the Bernoulli Equation here, there's no one half rho V squared term inside the house. And since, this height difference is very very small we're going to ignore the effect of this rho gh term, as well. So the force on this roof is going to be a result of the pressure difference between the inside and the outside. And so that pressure difference is going to be the force divided by the area and we'll solve for the force by multiplying both sides by A. And so we have force is the difference in pressure times area. The pressure inside is atmospheric pressure as I mentioned and that's the only term in the Bernoulli's Equation inside the house. And so, that's why this term is by itself. Then outside the house we have the pressure outside plus one half times the density of air times the speed of the air squared. And if we subtract Po from both sides, we got the difference in pressure, atmospheric pressure minus pressure outside is equal to this one half density of air times its air speed squared. And so this is we substitute in for delta P in our formula for the force. So the force is going to be one half rho V squared times area. So that's one half times 1.14 kilograms per cubic meter density times 45 meters per second squared times 220 square meters giving us 2.54 times ten to the five newtons will be the force on the roof and that will be a force upwards.

Comments

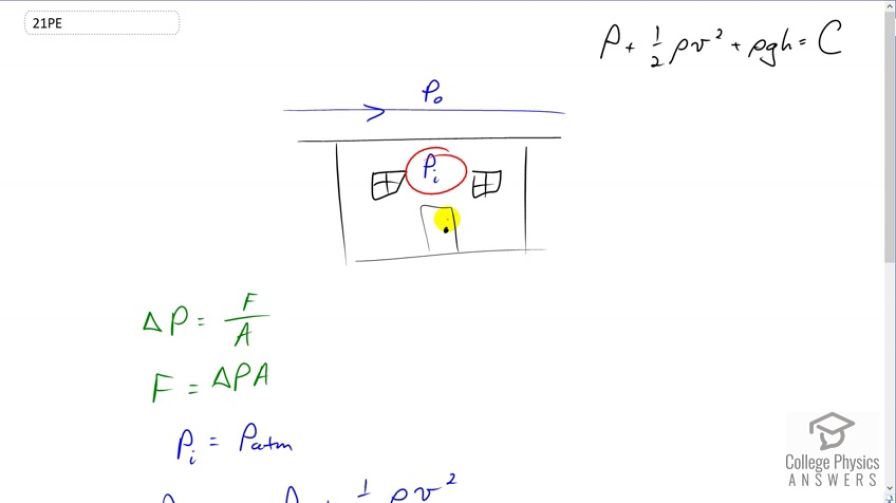
If you use the atmospheric pressure provided here to solve for P outside and then plug that into the P = F / A equation, you get a very different force a couple of magnitudes greater than the one you calculated. Just curious why you didn't use the Patm given in the stem?

Hi sfd228, thank you for the question. When plugging the atmospheric pressure in the house into P = F / A to find the force, the assumption being made is that there is a perfect vacuum outside the house, which of course is not the case. It's the pressure difference between inside the house vs. outside that results in a net force on the roof. The quickly moving air outside the house has a lower pressure as a result of its movement, so there's a net pressure pushing up on the roof since the pressure inside is still the original atmospheric pressure that exists with no air movement.
Hope this helps,
Shaun